金融考试代写 Risk Management and Financial Institutions

RM 432: Risk Management and Financial Institutions

金融考试代写 For this section, you will be using the S&P 500 index price data that is provided to you in the worksheet labeled “DataProblem4-6a

The assignment questions are to be completed within groups of two. Do not share your work with students from other groups. Only original work done by your group members are to be submitted. Plagiarism will not be tolerated in this class. The assignment will be marked based on (1) How you arrive at the solution, (2) Is the solution logical, consistent with the materials taught in class? (3) The presentation of your results. Remember, you must present your work in a clear and concise
manner. How you communicate your work visually and verbally matters. You are require to submit a spreadsheet with your calculations for the numerical questions and a separate document with the answer for the conceptual questions and where you show the key steps involved to get the solution of the numerical questions.

Assignment due: Feb 9th by 11:59 pm.

Question 1 (10 points)  金融考试代写

A company estimates that its profit over each calendar year is normally distributed with a mean of 1% of assets per year and the standard deviation of 2% of assets per year.

(a) (6 points) How much equity (as a percentage of assets) does the company currently need to have in order to be 99% sure that its equity will not fall below 5% of its assets at the end of two years.

(b) (4 points)If the company currently has equity that is 3% of its assets, what is the probability that all of its equity will be wiped out at the end of three years? Ignore taxes. Remember to show your work

Question 2 (20 points)

A portfolio manager estimates that the volatility of her daily portfolio returns is 1.2%. She also expects this portfolio to bring a return of 6% per year. Assume that there are 252 trading days in a year. The current value of her portfolio is $10,000,000.
(a) (5 points) Calculate a 5-day VaR ($) at the 97,5% confidence level
(b) (5 points) What is the 95% confidence interval of the value of this portfolio after 20 days?
(c) (5 points) Suppose the value of a portfolio dropped by $555,000 in 10 days. What is the chance of this happening?
(d) (5 points) Up to what horizons (number of days) can she hold this portfolio with a 99% confidence that her total loss will not be more than 30%? Show your work. State your answer in number of days

Question 3 (5 points)  金融考试代写

Suppose that in a GARCH(1,1) model, ω = 0.000003 (or 3*10 -6 ), α = 0.015, β = 0.97.
(a) (2 points) What is the long-run average daily variance? What is the long-run average monthly volatility? Assume that there are 21 trading days in a month.
(b) (3 points) If the current daily volatility is 0.5% per day, what is your estimate of the annualized volatility in 10, 30, and 50 days? Is your estimate increasing or decreasing in number of days? Briefly explain why it is increasing or decreasing.

Question 4 (10 points)

You will need the data set provided to you on Quercus. Use the data reported in the worksheet labeled “DataProblem4-6”. The data set contains the daily prices of the S&P500 index.
(a) (3 points) Compute annualized return and volatility. Express your results in percentage terms. Don’t forget that the data are in daily frequency and use logarithmic return when computing daily returns. That is

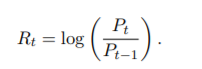
(b) (4 points) Plot daily returns over time. Compute 1-day and 10-day VaR at the 99% confidence level. Express VaR in percentage term
(c) (3 points) Compute 1-day Expected Shortfall (ES) of your portfolio at the 99 % confidence level using your estimated 1-day 99 % VaR from (ii). Assume that your portfolio return is normally distributed

Question 5 (15 points)  金融考试代写

We will test whether your 1-day VaR calculated from Question 4 is a good risk measure. Use the VaR calculated using the actual volatility of your portfolio returns (i.e., from (ii) in Q4). We will back test your 1-day VaR using the security prices from January 2001 to December 2010.

(a) (5 points) Report the number of times that 1-day 99% VaR of your portfolio is violated during 2001 - 2010. Calculate the violation rate of your 1-day VaR measure. If your VaR measure is good, what do you expect the violation rate to be?
(b) (5 points) Using the statistical method introduced in class, test whether your 1-day 99% VaR measure is an acceptable model. Show your work.
(c) (5 points) Based on the violations you observed in (a), compute 1-day Expected Shortfall (ES) of your portfolio at the 99% confidence level. Calculate it using empirical distribution. Compare the results that you calculated from Question 4. c.

Question 6 (10 points)

For this section, you will be using the S&P 500 index price data that is provided to you in the worksheet labeled “DataProblem4-6a”. The data contains S&P 500 index price from 2000 to 2010.
(a) (3 points) Explain what is the S&P 500 index? What kinds of firms are included in this index and who decides the composition of the index? Be concise with your answer.
(b) (7 points) Select two consecutive years of data from the S&P 500 price after 2001. For example, you may choose 2009-2010, etc. You can choose the years that interest you.

(i) Plot the cumulative S&P 500 returns over the two years that you choose.
(ii) Calculate daily variance of your selected S&P 500 returns data using the Risk Metric model. Now, assume the following parameters of GARCH (1,1) model: α = 0.12, β = 0.86, ω = 6.0E-07. Calculate daily variances of your selected S&P 500 returns data using GARCH (1,1) with the given parameters. Plot the time-series of the daily volatilities you calculated using the Risk Metric model and the GARCH (1,1) model on the same figure. Briefly comment on any similarities or differences
between the two volatility models

Question 7: Conceptual Questions (30 points)  金融考试代写

Answer the following questions:
(a) (8 points) Explain the concepts of Moral Hazard and Adverse Selection. Provide an example where these frictions manifest themselves in the case

(i) banks, (ii) insurance companies, and (iii) mutual funds. To be clear, you are required to provide one example of MH and one example of AS for each of the three cases.
(b) (6 points) Explain for each example you provided in (a), how we could mitigate the problem.
(c) (5 points) Explain why VaR is not a coherent measure. Which property does VaR not satisfy? Provide an example to show how VaR fails to satisfy this property.
(d) (3 points) What is the so-called Volcker rule? Explain the arguments in favor used by regulators, and the arguments against used it by banks.
(e) (6 points) Explain the concepts of (i) front running, (ii) late trading, and (iii) directed brokerage. Provide one example for each case of scandals related to these practices.
(f) (2 points) Explain the main differences between an index Mutual Fund and an ETF that follows the same index.

更多代写： HomeWork cs作业     金融代考    postgreSQL代写         IT assignment代写     统计代写    C语言程序设计代写