ECON3006/4437/8037: Financial Economics
金融经济学作业代写 Draw an Edgeworth box (indifference curves, initial endowment, equilibrium price from (b))(b) Specify via the Edgewort
1. [4+2+2=8 points] Consider a two agent economy with S = {1, 2, 3, 4} and 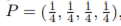 , utility 金融经济学作业代写
, utility 金融经济学作业代写

and endowments
ω1 = (2, 2, 2, 2) ω2 = (1, 1, 1, 4)
(a) Determine the Arrow-Debreu Equilibrium 金融经济学作业代写
![]()
(b) Explain the equilibrium outcome (risk sharing) based on risk preferences and initial endowments.
(c) Why can’t there be full insurance for both agents in equilibrium?
2. [2+2=4 points] Take the economy from part/question 1 but now with S = {1, 2}, and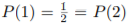 (“it turned out state 3, 4 are no longer possible”)
(“it turned out state 3, 4 are no longer possible”)
(a) Draw an Edgeworth box (indifference curves, initial endowment, equilibrium price from (b))
(b) Specify via the Edgeworth box the resulting Arrow-Debreu economy and the new equilibrium.
3. [2+1=3 points] Take the equilibrium state price p from part 1. (If 1. is not solved then take any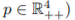 金融经济学作业代写
金融经济学作业代写
(a) Determine the risk-neutral probabilities from part 1.
(b) What is the price of the aggregate endowment, when priced under risk-neutral probabilities from (a)?
4. [4=(1+1)x2 points] Risk preferences: Compute the certainty equivalents of agent 1 and 2 from part 1 at their initial endowment. What are their risk premia?
5. [4 points] Find by computation a price q for the risky assets that are induced by the return matrix
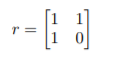
such that an equilibrium price p from part 2. is the (unique up positive scalars) arbitrage free state prices.
(If 2. is not solved then take any ![]() on the 45o -degree line.)
on the 45o -degree line.)





发表回复
要发表评论,您必须先登录。