逻辑与建模代写 Final Exam Logic and Modelling

Final Exam Logic and Modelling 2014

逻辑与建模代写 We want a terminating program P with the property that the output value (after execution) of x is the input value (before execution)

General information:  逻辑与建模代写

• The exam consists of 9 pages and 7 tasks (plus one bonus task).
• The maximal number of points is 100 (104 including 4 bonus points).
• The grade for this exam is the minimum of 10 and (points + bonus + 11)/11.

1. This task concerns validity, and (un)satisfiability in propositional and predicate logic. Tell for each of the formulas whether it is valid (tautology), satisfiable or a contradiction:
   (the answer suffices, no explanation is needed)
   (a) (a → b) → a (2 points)
   (b) (a → b) ∨ (b → a) (2 points)
   (c) ((a → b) → a) → ¬a (2 points)
   Answer the following:
   (d) What does it mean that a set of formulas (of predicate logic) is consistent? (3 points) Tell for each of the sets whether they are consistent:
   (the answer suffices, no explanation is needed)
   (e) { ∀xP(x) ∨ Q(x), ∃x ¬P(x), ∃x ¬Q(x) } (2 points)
   (f) { ∀x ∃y R(x, y), ∀x ∃y ¬R(x, y) } (2 points)
   (g) { ∀xS(k, x) → ¬S(x, x), ∀x¬S(k, x) → S(x, x)} (2 point)




2. This task concerns natural deduction and counter models. Determine for each of the given semantic implications whether it is valid.
   – For the valid implications, give a derivation using natural deduction.
   – For the invalid implications, give a counter model (in case of propositional logic give a truth assignment of the variables that shows that the implication is wrong).
   (a) a ∨ (b → c) |= (¬a ∧ b) → c (6 points)
   (b) ∀x ¬R(x, x) |= ∀x ∃y ¬R(x, y) (6 points)
   (c) ∀x ∀yR(x, y) → ¬R(y, x)|= ¬∃x R(x, x) (6 points)
   (d) ∀x ∃y R(x, y) |= ∃x ∃yR(x, y) ∧ R(y, x)(6 points)

3. This task concerns the translation of sentences in natural language to predicate logic (with or without equality). 逻辑与建模代写

The domain is a group of people. The meaning of the symbols is:
a : Alma K(x, y) : x knows y
g : Gustav L(x, y) : x loves y
H(x, y) : x was husband of y

Translate the following sentences into formulas of predicate logic (with or without equality).

(a) Everybody who knows Gustav also knows Alma. (3 points)
(b) Not all of Alma’s lovers’ lovers love her. (3 points)
(c) Alma had two (or more) husbands. (3 points)
(d) Apart from Gustav, Alma had precisely two other husbands. (4 points)

1. This task concerns basic modal logic and Kripke structures. Given is the Kripke model M = (W, R, L) as drawn in the following figure:

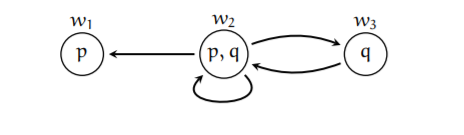
Determine for each world x whether or not the following holds:
(the answer suffices, no explanation is needed)
(a) M, x ✸p → p (3 points)
(b) M, x ✷✷q (3 points)
We now consider the underlying frame F = (W, R). Determine whether:
(the answer suffices, no explanation is needed)
(c) F |= ✸p → ✸✸p (2 points)
(d) F |= (p ∧ q) → ✸q (2 points)
The following task is about correspondence of p → ✸p with reflexivity:
(e) Show that for every frame F that is not reflexive: F 6|= p → ✸p. Please give a detailed argumentation, as has been used in the lectures. (4 points)

5. This task concerns meta-theorems of predicate logic, and expressibility of properties in predicate logic.

(a) Formulate the compactness theorem of predicate logic. (3 points)
(b) Exhibit, for n = 2, n = 3, and schematically for general n, formulas φn in predicate logic with equality such that, for all n ∈ N, n ≥ 2, the formula φn is true in a model M if and only the domain of M contains at least n values. (4 points)
(c) Explain the structure of the argument for why model finiteness is not expressible by a formula in predicate logic. (A proof sketch is sufficient that may contain ‘then it can be shown that . . . ’ at places provided that the basic argument is clear as well as the statements that are used, and the theorem(s) that are applied.) (5 points)

6. This task concerns decision problems and their solvability (decidability).  逻辑与建模代写

(a) When is a decision problem decidable (solvable)? (3 points)
(b) Give an instance of Post’s Correspondence Problem (PCP) that has a solution (tuple of indices) of length at least 4 with at least one repetition of indices. Clearly specify the instance as well as the solution. (4 points)
(c) Is the decision problem for entailment statements Γ ` φ, where Γ is a finite set of formulas of predicate logic and φ a formula of predicate logic, decidable (solvable)? Justify your answer by linking this question to the answer for the analogous question concerning formula validity. (4 points)

7. This task concerns program logic.

We want a terminating program P with the property that the output value (after execution) of x is the input value (before execution) of y plus 1, and the output value of y is the input value of x.

(a) Formulate this program specification for P as an appropriate satisfiability statement concerning a Hoare triple. (3 points)
(b) Give a core language program that implements this program specification. (3 points)
(c) Which rules of the proof system for partial correctness will be used in a proof of partial correctness of your program? Pick one of these rules, exhibit it formally, and explain, best in one sentence, how this rule can be understood. (5 points)

1. (Bonus task) This task concerns satisfiability of a formula of predicate logic. The formula ∃x∀yS(x, y) ↔ ¬S(y, y) expresses the existence of a barber in Russell’s
   Barber Paradox: a man who shaves precisely all men who do not shave themselves. Show that this formula is unsatisfiable. Use an argumentation that analyses the interpretation of this formula in arbitrary models M with respect to arbitrary environments `. (4 points）

更多代写： HomeWork cs作业     金融代考    postgreSQL代写         IT assignment代写     统计代写    计算机分布式系统代写