财务建模 – Financial Modeling – 英国数据代写

Financial Modeling

财务建模

财务建模  In the view of Jenkins (2006), the autoregressive integrated moving average (ARIMA) model is one of the important model classes that..

a) Quarterly GDP Data for Austria

In the view of Jenkins (2006), the autoregressive integrated moving average (ARIMA) model is one of the important model classes that are used to describe s single time series. The assignment chooses this model to analyze the time series secondary data of a country. For this purpose, the assignment chooses Austria; an OECD nation and collect the quarterly GDP data for the last fifty years i.e. 1963 - 2013. The assignment uses STATA software as a base to perform time series test and graphical analysis in order to predict the quarterly GDP of Austria for the coming 50 years.

b) Time Series Plot

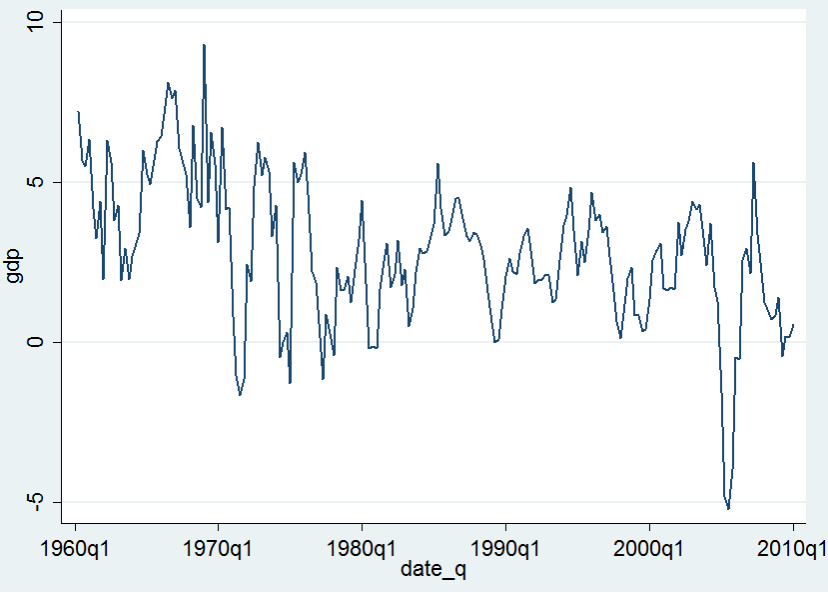
In Stata, simple time series command is used to plot the trend line of Austria’s quarterly GDP over the last 50 years. The graph below provides the trend line of quarterly GDP rates as change over the same quarter and analysis shows downward GDP movement during the economic crisis of 2007-2009.

译文：a) 奥地利的季度 GDP 数据  财务建模 

在 Jenkins (2006) 看来，自回归综合移动平均 (ARIMA) 模型是用于描述单个时间序列的重要模型类之一。 作业选择这个模型来分析一个国家的时间序列二手数据。 为此，任务选择了奥地利； 一个经合组织国家，收集过去 50 年（即 1963 - 2013 年）的季度 GDP 数据。该任务使用 STATA 软件作为基础进行时间序列测试和图形分析，以预测奥地利未来 50 年的季度 GDP。

b) 时间序列图

在 Stata 中，简单的时间序列命令用于绘制奥地利过去 50 年季度 GDP 的趋势线。 下图提供了季度 GDP 率随同季度变化的趋势线，分析显示 2007-2009 年经济危机期间 GDP 下降趋势。

Graph 1: Quarterly GDP Growth Rates of Austria

(Source: OECD, 2015)

A look at the graph below, however, depicts an upward movement with slight variations during the crisis period. The graph below depicts a rather sharp trend of GDP.

译文：图 1：奥地利季度 GDP 增长率    财务建模 

（来源：经合组织，2015）

然而，下图显示了危机期间略有变化的向上运动。 下图描绘了一个相当尖锐的 GDP 趋势。

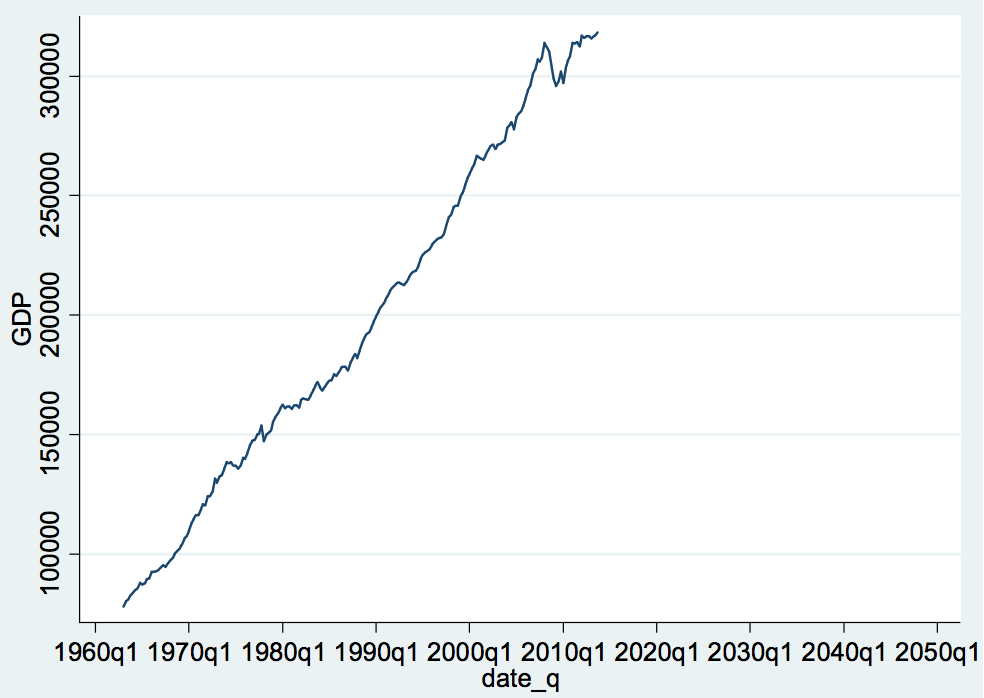
Graph 2: Quarterly GDP Trend

For better understanding, log function is used on the GDP data; the graph below shows that Austrian economy’s connection with the European Union State members had significant affect on the GDP performance of the country. As a consequence of 2007-08 crises, Austrian GDP reported variations in the late 2009; however, the graph below depicts a visible recovery of Austrian economy due to subsidized government projects. Nonetheless, time series analysis shows that the GDP trend is non-stationary and non-static over the given time period.

译文：图 2：季度 GDP 趋势  财务建模

为了更好地理解，对 GDP 数据使用 log 函数； 下图显示，奥地利经济与欧盟成员国的联系对该国的 GDP 表现产生了重大影响。 由于 2007-08 年的危机，奥地利的 GDP 报告在 2009 年末出现了变化； 然而，下图描绘了由于政府项目的补贴，奥地利经济明显复苏。 尽管如此，时间序列分析表明，在给定的时间段内，GDP 趋势是非平稳和非静态的。

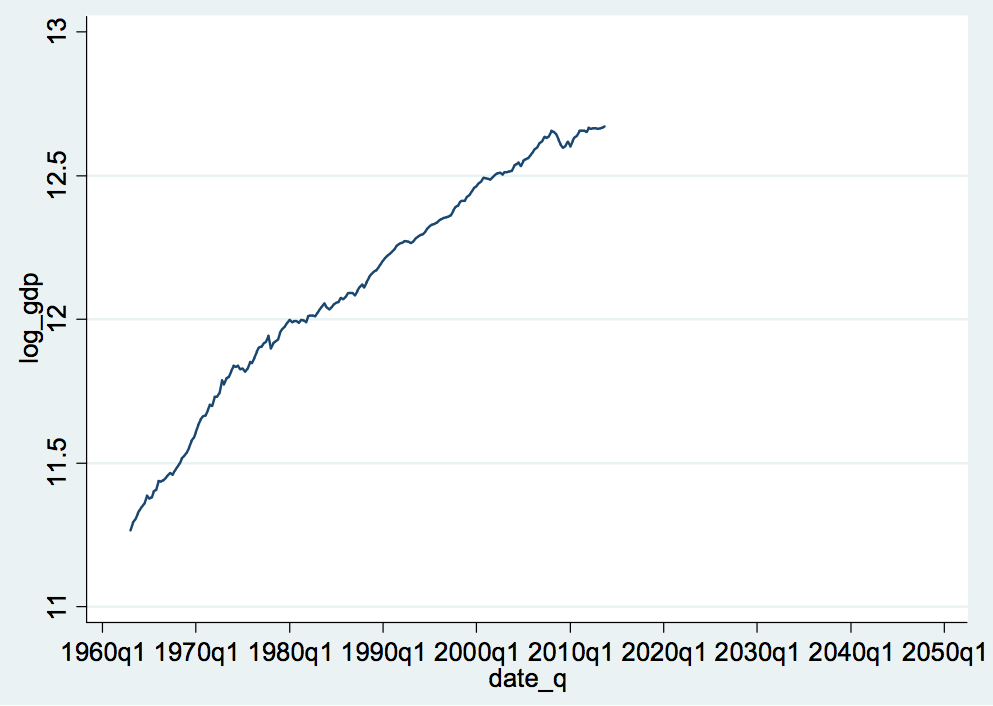
Graph 3: Trend of Log_GDP

c) Autocorrelation Function (ACF) and the Order of AR and MA

In the Dickey-Fuller test, if test statistic is greater than all the values at three different critical levels then the null hypothesis can be rejected. Stata results in the figure below depict an opposite situation as the test statistics value is -0.175 and it is small than the three critical values i.e. -3.476 at 1%, -2.883 at 5% and -2.573 at 10%. In other words, Dickey-Fuller unit root test indicates that the null hypothesis of GDP series cannot be rejected.

译文：图3：Log_GDP趋势

c) 自相关函数 (ACF) 和 AR 和 MA 的阶  财务建模 

在 Dickey-Fuller 检验中，如果检验统计量大于三个不同临界水平的所有值，则可以拒绝原假设。 下图中的 Stata 结果描述了相反的情况，因为测试统计值是 -0.175，它小于三个临界值，即 1% 时的 -3.476、5% 时的 -2.883 和 10% 时的 -2.573。 换句话说，Dickey-Fuller 单位根检验表明不能拒绝 GDP 序列的原假设。

Figure 1: Dickey-Fuller Test

The above illustration provides an indication for the presence of unit root problem, which is solved through the first differential (See figure below). For this purpose, Dickey-Fuller test is re-performed with the first differential; this turns the non-stationary GDP series into a stationary series. The figure below shows that test statistics value is smaller than all the three critical values; hence, the series is stationary.

译文：图 1：Dickey-Fuller 测试  财务建模 

上图表明存在单位根问题，该问题通过一阶微分解决（见下图）。 为此，使用一阶微分重新执行 Dickey-Fuller 检验； 这将非平稳 GDP 序列变为平稳序列。 下图显示测试统计值小于所有三个临界值； 因此，该系列是平稳的。

Figure 2: Dickey-Fuller with First Differential

The auto-correlation graph (Ac) below provides evidence for the presence of higher lag in the data.

译文：图 2：具有一阶差分的 Dickey-Fuller

下面的自相关图 (Ac) 提供了数据中存在较高滞后的证据。

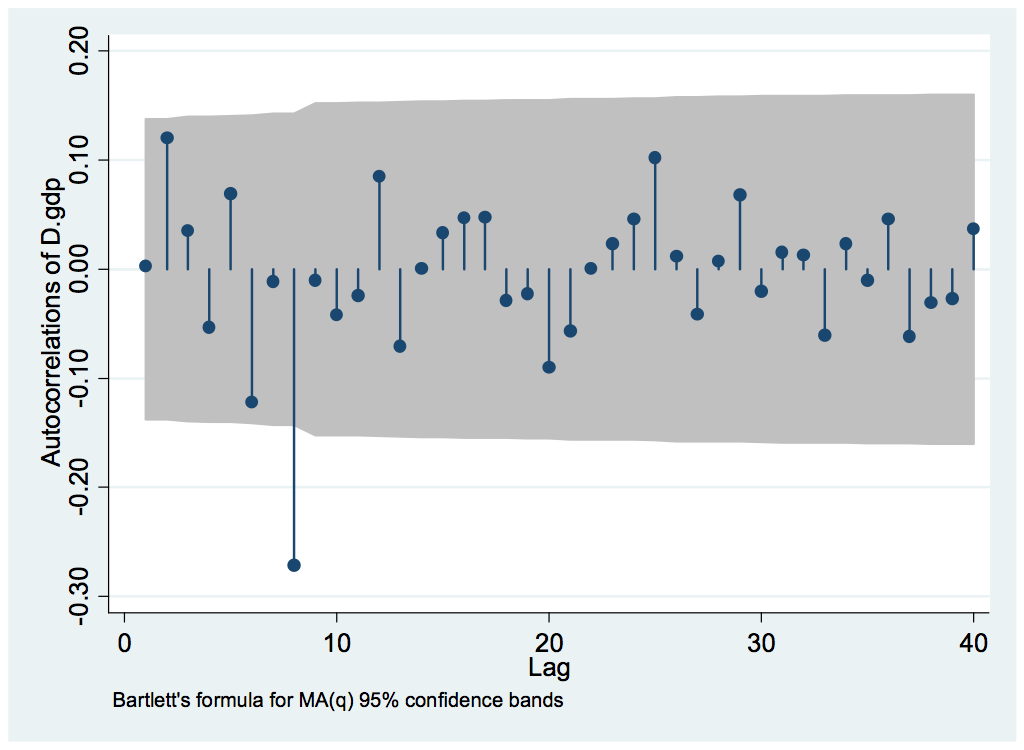
Graph 4: AC

i. Partial Autocorrelation Function (PACF) Plot

In line with Ac results, the Pac plot below also depicts higher lags, which means that the stationary series achieved through first differential above is providing insignificant values.

译文：图 4：交流电  财务建模 

一世。 偏自相关函数 (PACF) 图

与 Ac 结果一致，下面的 Pac 图也描绘了更高的滞后，这意味着通过上面的一阶微分获得的平稳序列提供的值不重要。

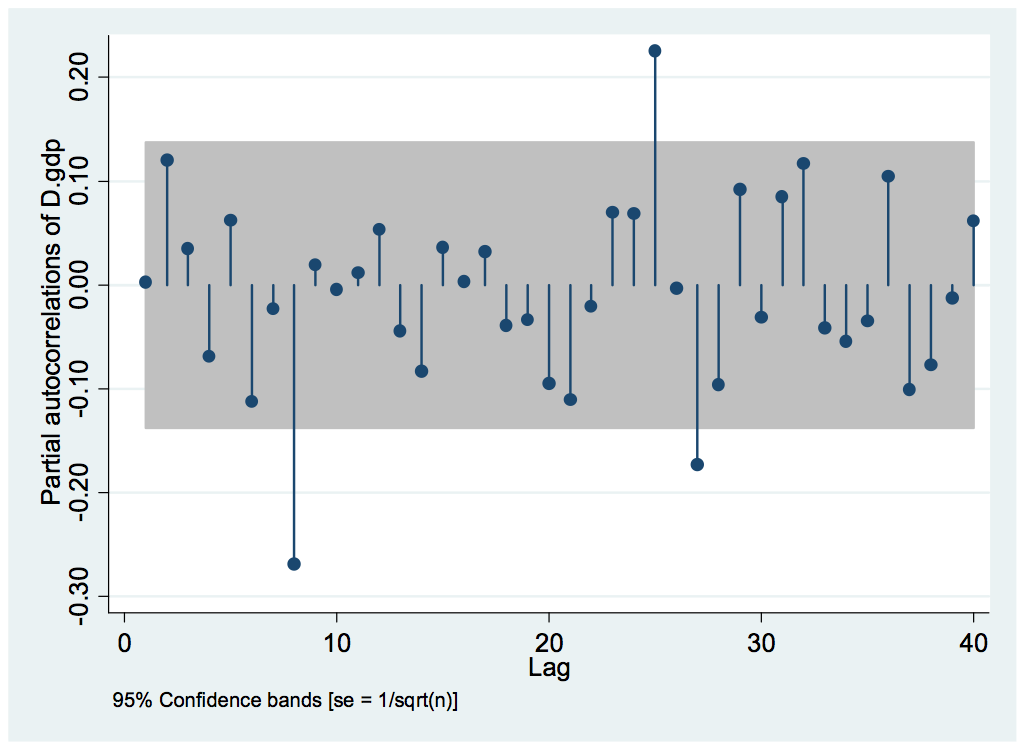
Graph 5: Pac

In order to choose the right type of ARIMA model, log_gdp command is performed in the Stata software. As can be seen in the figure below, z(t) value is lower than the standard value i.e. 0.05; this means that the series is stationary and the model selected for evaluation is Arima model with D=0.

译文：图 5：Pac

为了选择正确的 ARIMA 模型类型，在 Stata 软件中执行 log_gdp 命令。 如下图所示，z(t)值低于标准值即0.05； 这意味着该系列是平稳的，并且选择用于评估的模型是 D=0 的 Arima 模型。

Figure 3: Dickey-Fuller log_GDP  财务建模 

The choice of model can be justified through Ac and Pac plots below, for example, the Ac graph below depicts gradual decline. Analysis shows significant values till the 16^th lag and these are certainly different from zero.

译文：图 3：Dickey-Fuller log_GDP

模型的选择可以通过下面的 Ac 和 Pac 图来证明，例如，下面的 Ac 图描绘了逐渐下降。 分析显示直到第 16 次滞后为止的重要值，并且这些值肯定不同于零。

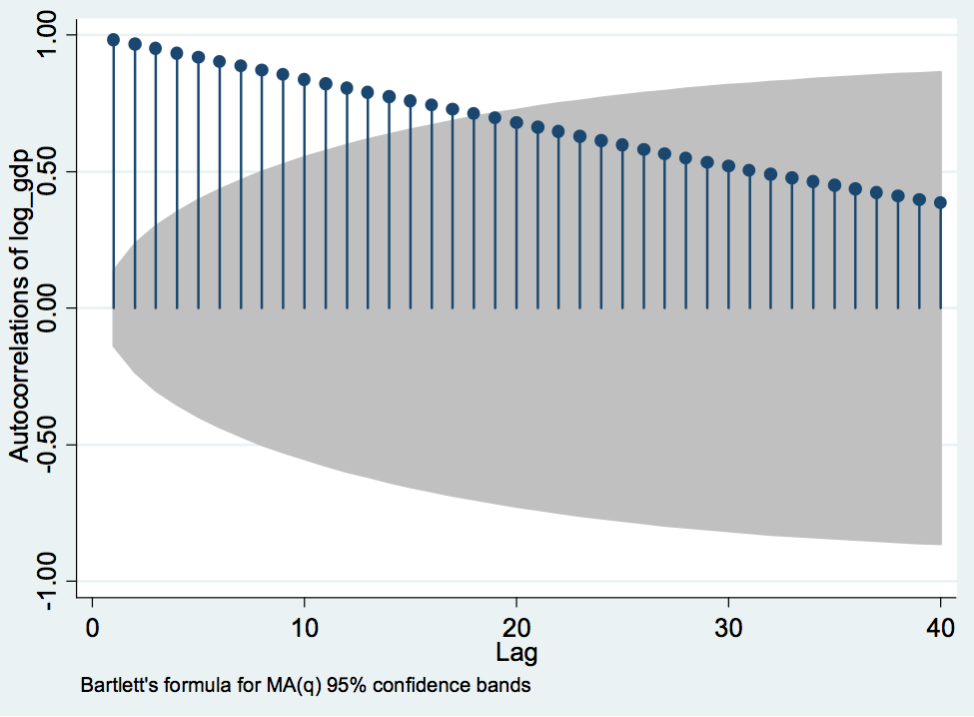
Graph 6: Autocorrelation

The Pac graph below provides clear evidence of partial coefficient at points such as lag 1 and 9; thus, values at these lag points are significant and outside the 95% confidence interval. In contrast, other lags report insignificant values; hence, p-value for Arima model is suggested to be 1.

译文：图 6：自相关  财务建模 

下面的 Pac 图清楚地证明了滞后 1 和 9 等点的部分系数； 因此，这些滞后点的值是显着的并且在 95% 置信区间之外。 相比之下，其他滞后报告的值不重要； 因此，Arima 模型的 p 值建议为 1。

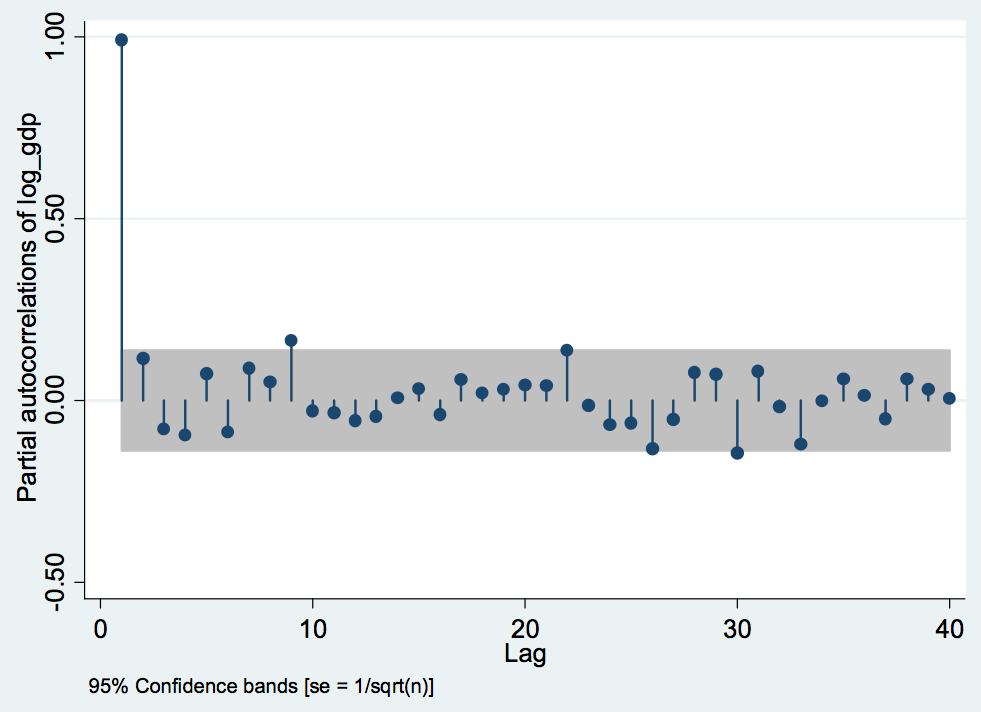
Graph 7: Partial Autocorrelation

d) Type of ARIMA Model and Rationale

Since the above testing provides one significant point in Pac plot and declining trend of Ac, the proposed ARIMA(p,d,q) is ARIMA(1,0,0). Normally, appropriate model is done through the AIC or BIC testing (Tsay, 2010); however, in the present context, the thumb rule of selecting the model with the lowest value may not be applicable. Keeping this into consideration, ARIMA(1,0,0) with Dickey-Fuller with log is selected as the appropriate model type because the above tests depict only one model i.e. ARIMA(1,0,0).

译文：图 7：偏自相关    财务建模 

d) ARIMA 模型的类型和基本原理

由于上述测试提供了 Pac 图中的一个重要点和 Ac 的下降趋势，因此建议的 ARIMA(p,d,q) 为 ARIMA(1,0,0)。 通常，适当的模型是通过 AIC 或 BIC 测试完成的（Tsay，2010）； 然而，在目前的情况下，选择具有最低值的模型的经验法则可能不适用。 考虑到这一点，选择带有对数的 Dickey-Fuller 的 ARIMA(1,0,0) 作为适当的模型类型，因为上述测试仅描述了一个模型，即 ARIMA(1,0,0)。

Figure 4: AIC

Figure 5: Portmanteau Test

e) Forecasting the GDP Growth

In the Stata, following commands are used to create a forecast the GDP of Austria over the next fifty years.

译文：图 5：Portmanteau 测试  财务建模 

e) 预测 GDP 增长

在 Stata 中，以下命令用于创建奥地利未来五十年的 GDP 预测。

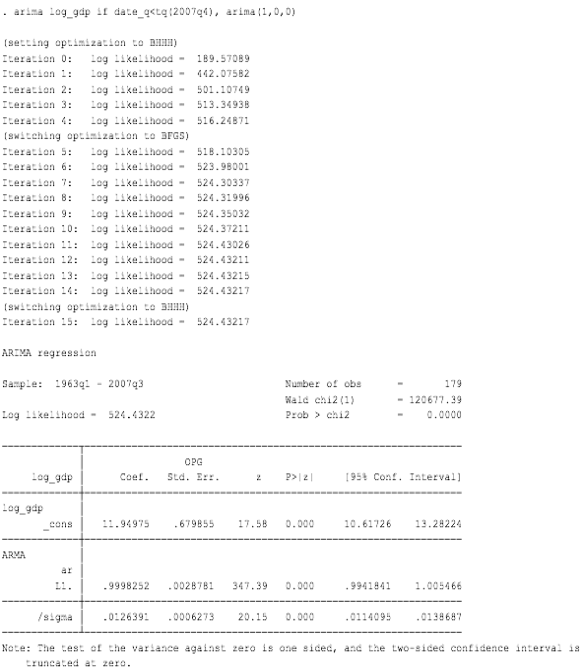
Figure 6: Forecasting Command

As illustrated in the graph below, Austrian GDP is expected to remain flat and stable in the coming fifty years; hence, the trend is plotted as a straight line. Since the model intends to study the effect of financial crisis on the forecast, ARIMA 2007 model is applied. The graph below forecasts the GDP trend with the influence of crisis.

译文：图 6：预测命令  财务建模 

如下图所示，奥地利的 GDP 预计在未来 50 年将保持持平和稳定； 因此，趋势被绘制为一条直线。 由于该模型旨在研究金融危机对预测的影响，因此采用了 ARIMA 2007 模型。 下图预测了受危机影响的GDP趋势。

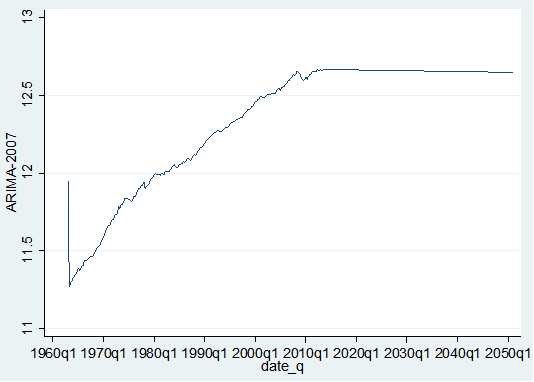
Graph 8: ARIMA 2007

According to analysis, Austria’s GDP remained under the sharp influence of economic crisis; evidence to the notion can be taken from the sharp GDP decline from 12.62% (2007) to 0.02% (2008).

译文：图 8：ARIMA 2007  财务建模 

据分析，奥地利的GDP仍受经济危机的严重影响； 可以从 GDP 从 12.62%（2007 年）急剧下降到 0.02%（2008 年）中得出这一观点的证据。

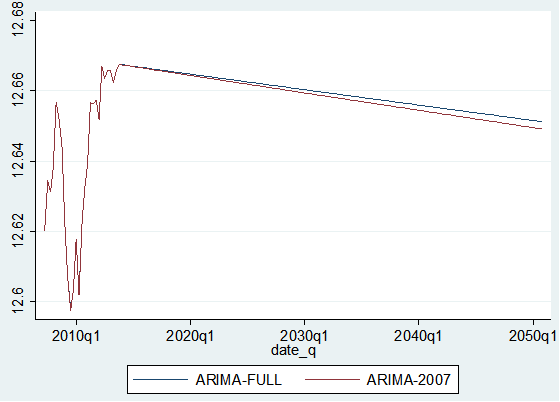
Graph 9: ARIMA Full and ARIMA 2007

In the graph above, ARIMA FULL line moves above the ARIMA 2007 line; since ARIMA FULL values are higher than ARIMA 2007; the evaluation suggests that unlike ARIMA 2007, ARIMA FULL line indicates no impact of financial crisis on Austria’s GDP.

f) The Monte-Carlo Experiment  财务建模

Following are the commands to prove the statement that Dickey-Fuller model may not be suitable for stationary series if the model is based on time trend.

译文：图 9：ARIMA Full 和 ARIMA 2007  财务建模 

在上图中，ARIMA FULL 线移动到 ARIMA 2007 线上方； 因为 ARIMA FULL 值高于 ARIMA 2007； 评估表明，与 ARIMA 2007 不同，ARIMA FULL 线表明金融危机对奥地利的 GDP 没有影响。

f) 蒙特卡罗实验

以下是证明如果模型是基于时间趋势的 Dickey-Fuller 模型可能不适用于平稳序列的说法的命令。

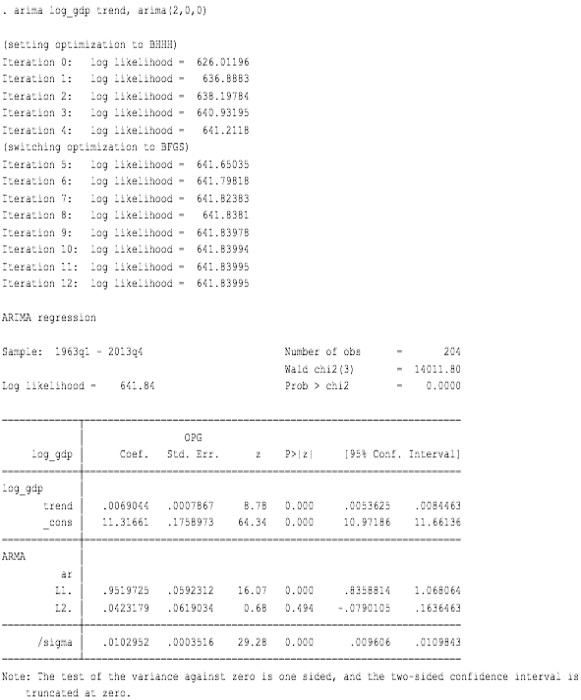
Figure 7: Simulation

At x=0, the p-vale is 95.8%, which means the Dickey-Fuller test with no trend is more reliable than otherwise. The figure below indicates that the Dickey-Fuller value at x=1 is significant; however, p-value is only significant for 4.2% of the total 1000 frequency. Hence, in case of trend model, Dickey-Fuller is less suitable.

译文：图 7：模拟    财务建模 

在 x=0 时，p 值为 95.8%，这意味着没有趋势的 Dickey-Fuller 检验比其他检验更可靠。 下图表明 x=1 处的 Dickey-Fuller 值是显着的； 然而，p 值仅对总 1000 频率的 4.2% 显着。 因此，在趋势模型的情况下，Dickey-Fuller 不太适合。

Figure 8: Simulation Results

On a simple note, the evaluation suggests that the Dickey-Fuller test with trend model is less suitable for stationary test and it cannot be relied as the results are very weak.

译文：图 8：仿真结果

简而言之，评估表明带有趋势模型的 Dickey-Fuller 检验不太适合静态检验，并且由于结果非常弱而不能信赖。

References

Jenkins, M. G. (2006). Autoregressive–Integrated Moving Average (ARIMA) Models, in Encyclopedia of Statistical Sciences, 1-6.

OECD. (2015). Quarterly National Accounts. [online] Available from <https://stats.oecd.org/index.aspx?queryid=350#> [28^th April 15]

Tsay, S. R. (2010). Analysis of Financial Time Series. New Jersey: John Wiley & Sons.

商科代写    cs代写   法律学代写   经济学代考   艺术代写   心理学代写