经济学数学代考 4SSMN901 Mathematics For Economists

4SSMN901 Mathematics For Economists

经济学数学代考 The government decides to impose a tax per unit on each good, denoted τA and τB, respectively. The tax is levied on consumers.

This paper is part of an examination and counts towards the award of a degree. Examinations are governed by the College Regulations under the authority of the Academic Board.

Assessment Format: 4SSMN901 Examination 2020/21

Module code and title: 4SSMN901 Mathematics For Economists

Examination Period: Period 1, January 2021 Time allowed: Students should spend no longer than 2 – 3 hours on this paper. The paper will be available for 24-hours from 10:00am GMT on 11 th January 2020. Students will need to submit their answers by 10:00am GMT 12th January 2020.

INSTRUCTIONS TO CANDIDATES:  经济学数学代考

1. There are 8 questions in total. You must answer all questions. The first 7 questions should be submitted as part of the written exam submission and Question 8 should be submitted separately as the video submission.




2. Paste any required diagrams and graphs for your answers directly onto the answer sheet using software or uploaded photos for the written exam submission.




3. A template answer sheet has been provided on the KEATS page, you should complete the first page ‘cover sheet’ and then type your answers below for the written exam submission. Make sure you clearly indicate the questions you are answering (e.g. Section A, Question 1). Round up the answers to 2 decimals.




4. For the video submission, you should attach the cover sheet as a separate document as part of your submission.




5. If you have a PAA cover sheet, you should include this in addition to the template answer sheet.




6. Save your work regularly, at least every 15 minutes.

ONLINE SUBMISSION INSTRUCTIONS:

1. Your answer sheet for the written exam submission should be submitted via the written exam Turnitin submission link on the module KEATS page.


2. Your video submission should be submitted via the video submission link on the module KEATS page.
   King’s Business School, King’s College London


3. Ensure your assessments are submitted for both the written exam and video submissions with the title CANDIDATE ID – MODULE CODE- e.g. AB12345-4SSMN901.


4. Once submitted, please check you are satisfied with the uploaded assessments via the relevant submission links.


5. If you experience technical difficulties uploading your assessments to KEATS please email a copy to UGBusiness@kcl.ac.uk with the subject of the email as CANDIDATE ID- MODULE CODE- PERIOD 1 ASSESSMENT. You should attach supporting evidence of technical issues where possible.

Q1. A sole producer has a marginal revenue function given by:

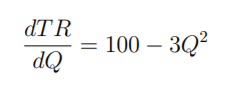
Is demand elastic or inelastic if they produce 5 units? 经济学数学代考

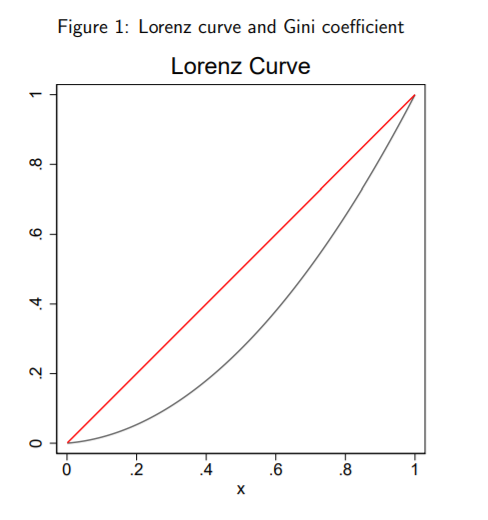
Q2. The Gini coefficient is a number between 0 and 1 and is used for measuring inequality. A number closer to 1 indicates higher inequality. Graphically, the Gini coefficient is given by the area between a diagonal straight line with slope equal to 1 and the Lorenz curve and this figure divided by the area below the diagonal. If The Lorenz curve is given by , estimate the inequality (up to 4 decimals). Compute the Gini coefficient. Is this an equal or unequal society? Figure 1 represents the diagonal straight line in red and the Lorenz curve in gray.

Q3. Demand is given by (P + 10)(Q + 20) = 1000 and supply by Q − 4P + 10 = 0. Determine the equilibrium, show it graphically as accurately as possible and determine the consumer surplus (round up to the nearest integer). How will this surplus be affected if price increases by 2 and the equilibrium is not realized?

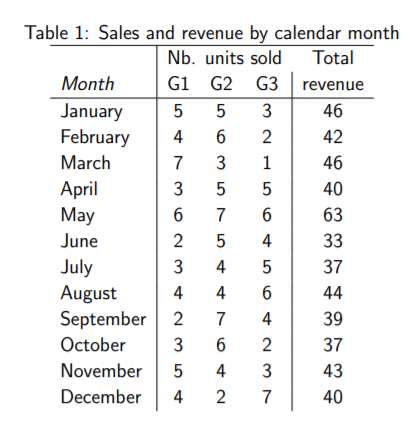
Q4. A firm produces three goods (G1, G2, G3) and sells them in a perfectly competitive market. Table 1 shows the number of units (in thousands) sold of each good along with the total revenue (in 1,000$) the firm raised by these sales in each calendar month of 2019. Find the equilibrium prices of these goods using matrices.

Q5. The demand functions for product A and B are each a function of the prices of A and B and are given by:  经济学数学代考

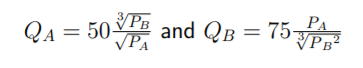
Determine whether A and B are competitive products, complementary products, or neither.

Q6. Suppose A and B are the only two firms in the market selling the same product. The industry demand for the product is p = 92 − qA − qB Where qA and qB denote the output produced and sold by A and  . Suppose the firms decide to enter into an agreement on output and price control by jointly acting as a monopoly. In this case, we say they enter into collusion. Show that the profit function for the monopoly is given by Π = pqA − cA + pqB − cB Express Π as a function of qA and qB, and determine how output should be allocated so as to maximise the profit of the monopoly

Q7. Pankaj is a junior web developer working for a major company. He divides his income between the consumption of goods x1, x2, and x3 and paying his rent. He can afford to buy one unit of x1 by working for one hour, 1 unit of x2 by working for two hours, and one unit of x3 by working for three hours. His rent costs him
40% of his income.

His utility function is given by:  经济学数学代考

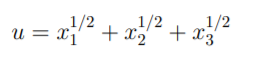
Assuming that Pankaj works for 40 hours a week:

i. Write down Pankaj’s weekly budget constraint and briefly describe his maximisation problem;
ii. Set up the Lagrangian and find how many of x1, x2, and x3 he would consume per week to maximise his well-being;
iii. What is the interpretation of the Lagrange multiplier? What does it tell us in this particular example?

iv. Imagine that the government raises a per-unit tax on good 2, which equals to 50% of its initial price. Discuss how this would change his optimal consumption levels of these three goods.
v. Imagine that Pankaj gets a promotion and becomes as senior web developer, which increases his hourly wage by 50%. Discuss how this would change his optimal consumption levels of these three goods.

Q8. [Video] Please answer to the question below in a short video about 5 minutes. You will need to submit the link to your video via the appropriate submission link on the KEATS page. Explain clearly and in detail, the steps you take to reach the solution. In particular, explain how you set up the question, why you do what you do in each step.

For example, “In this question, we find the optimal levels of consumption of good 1 and good 2 that will maximise the utility of X, which is given
by the function, subject to the following budget constraint. In order to solve this optimisation question, we start by writing the Lagrangian function by doing x and y. Then, we check the firstorder conditions... etc”. The goal here is for you to describe what you are doing and why. You could skip the steps involving manipulation of equations to reach parts of the solution. State clearly your key findings. For example, “By using equation (1) and (2) we can find that the optimal consumption level of good 1 is a and that of good 2 is b”.

Question: There are two goods, A and B, sold in an economy. The supply and demand equations of good A is given by:

PA = QA,S + 20
PA = −2QA,D + 50

The supply and demand equations of good B are given by:
PB = QB,S + 20
PB = −QB,D + 40

The government decides to impose a tax per unit on each good, denoted τA and τB, respectively. The tax is levied on consumers. i. Write down the total government revenue function and find the tax rates τA and τB, imposed on goods A and B respectively, that the government should charge to maximise its revenue? Show that these tax rates indeed maximise the government revenue. ii. Does the government charge the same per-unit tax rate on both goods? If there is a discrepancy, explain why it charges more in a given market than the other, linking your answer to the demand elasticities of the goods.

更多代写： HomeWork cs作业     金融代考    postgreSQL代写         IT assignment代写     统计代写  商务Assignment代写