Economics 3382A-001 Problem Set 6: Solutions
经济作业代做 Some notation: A strategy for each player is a triple of actions where the Örst entry is her action in the beginning of the game
Problem 1 经济作业代做
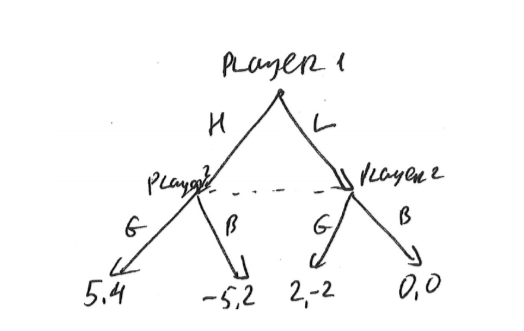
Since the players move simultaneously, their strategies are: H & L for #1, and G & B for
#2. The best responses are given here:
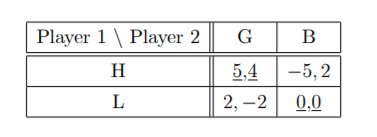
Thus there are two pure strategy NE (=mutual best responses): (H; G) & (L; B).
This game has only one subgame: the whole game. Subgame perfect equilibrium (SPE) is strategy proÖle that induces NE in every subgame. Thus there are two pure strategy SPE:
(H; G) & (L; B

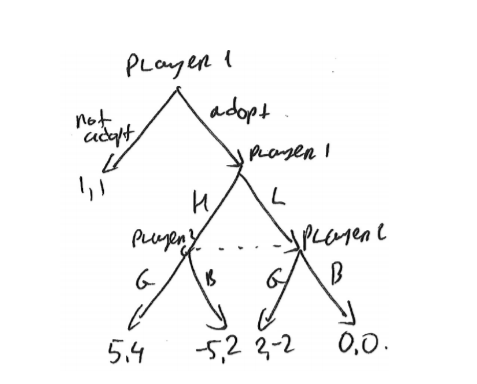
This game has two proper subgames: the whole game, and the part of the game after #1 chose "to adopt".
(c) As in part (a) #2 has only two strategies: G & B. #1 makes a choice between "adopt" & "not adopt" in the beginning of the game, and between H & L after "adopt". Thus she has four strategies: (adopt; H), (adopt; L), (not adopt; H);(not adopt; L). The corresponding matrix of payo§s with best responses is
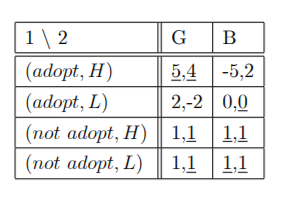
Thus there are three pure strategy NE: ((adopt; H); G), ((not adopt; H); B), ((not adopt; L); B).
Subgame perfect equilibrium (SPE) is strategy proÖle that induces NE in every subgame. From part (a) we know that the subgame after #1 chooses "adopt" has two NE: (H; G) & (L; B). Thus there are two pure strategy SPE: ((adopt; H); G), ((not adopt; L); B). Problem 2
(a) In the Örst stage game:
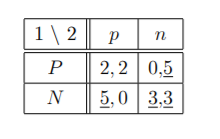
there is one pure NE (N; n). In the second stage game:
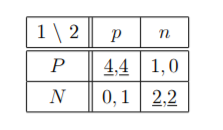
there two pure NE (P; p) and (N; n).
(b) There are 5 subgames: the overall game and 4 second-period games after (P; p), (P; n), (N; p) and (N; n) happen in the Örst stage. Strategy of a player consist of 5 actions: action to be taken in the Örst stage, and four actions to be taken in the second stage after (P; p),
(P; n), (N; p) and (N; n) happen in the Örst stage.
From part (a) we know that each of the 4 second-period subgames has two pure NE: (P; p)
and (N; n). Since our goal is to Önd (pure strategy) subgame perfect equilibrium (SPE) of the overall game, we will be looking only for NE of the overall game that are consistent with the players playing one of the two pure NE in each of the 4 second-period subgames. Suppose there is a pure SPE in which the players choose (P; p) in the Örst stage.
Letís Örst suppose that in the second-period subgame after (P; p) happens in the Örst stage we have NE (P; p). 经济作业代做
Then the equilibrium payo§ of each player in the overall game is 2 + 4 = 6. Consider player 1 deviating to N in period 1. Then, depending on whether (P; p) or (N; n) will be played after (N; p) happens in the Örst stage, her payo§ in the overall game will be either 5 + 4 = 9 or 5 + 2 = 7. In both cases it is a proÖtable deviation, and thus there is no such SPE.
The case when in the second-period subgame NE (N; n) is played after (P; p) happens in the Örst stage is similar. Hence there are no pure SPE in which the players choose (P; p) in the Örst stage.
(c) Suppose there is a pure SPE in which the players choose (N; n) in the Örst stage. Letís Örst suppose that in the second-period subgame after (N; n) happens in the Örst stage we have NE (P; p). Then the equilibrium payo§ of each player in the overall game is 3 + 4 = 7. Consider player 1 deviating to P in period 1. Then, depending on whether (P; p) or (N; n) will be played after (P; p) happens in the Örst stage, her payo§ in the overall game will be either 0 + 4 = 4 or 0 + 2 = 2. In both cases such a deviation is unproÖtable. The argument for player 2 is symmetric.
The case when in the second-period subgame after (N; n) happens in the Örst stage we have NE (N; n) is similar.
Hence there are many SPE in which the players choose (N; n) in the Örst stage: all strategy pairs that prescribe (N; n) in the Örst stage, and either (P; p) or (N; n) after (P; p) happen in the Örst stage, (P; p) or (N; n) after (P; n) happen in the Örst stage, (P; p) or (N; n) after (N; p) happen in the Örst stage, and (P; p) or (N; n) after (N; n) happen in the Örst stage. (Total of 16 SPE).
(d) Suppose there is a pure SPE in which the players choose (P; n) in the Örst stage. Letís Örst suppose that in the second-period subgame after (P; n) happens in the Örst stage we have NE (P; p) . Then the equilibrium payo§ of player 1 in the overall game is 0 + 4 = 4. Consider player 1 deviating to N in period 1. Then, depending on whether (P; p) or (N; n) will be played after (N; n) happens in the Örst stage, her payo§ in the overall game will be either 3 + 4 = 7 or 3 + 2 = 5. In both cases it is a proÖtable deviation, and thus there is no such SPE.
The case when in the second-period subgame after (P; n) happens in the Örst stage we have NE (N; n) is similar. Hence there are no pure SPE in which the players choose (P; n) in the Örst stage.
Problem 3 经济作业代做
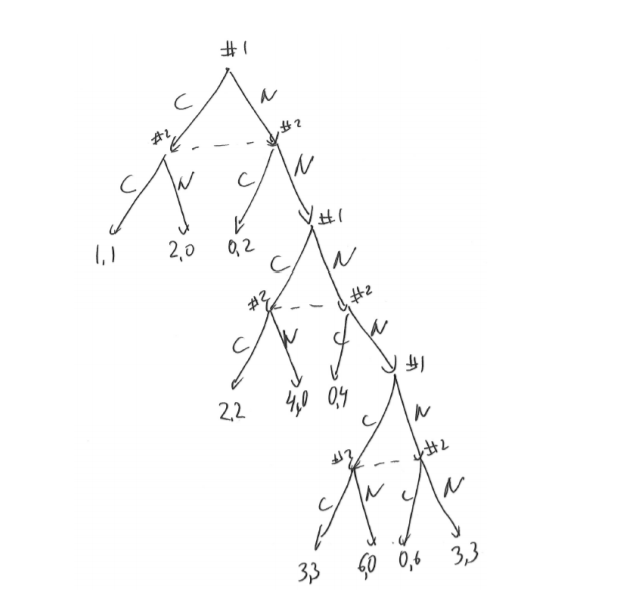
(b) Some notation: A strategy for each player is a triple of actions where the Örst entry is her action in the beginning of the game, the second ñafter (N; N) happened in t=1, and the third ñafter (N; N) and (N; N) happened in t=1 and 2. First, consider the subgame after (N; N) and (N; N) happened in t=1 and 2:
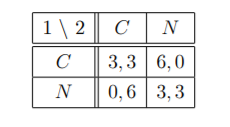
There is only one NE, (C; C), in this subgame (and it is in dominant actions). The playersí payo§s are (3; 3).
Next, consider the subgame after (N; N) happened in t=1. Since our goal is to Önd SPE of the overall game, we will be looking only for NE of this subgame in strategies that prescribe for the players to play (C; C) in the event that the third period is reached (i.e. if the players play (N; N) in t=2). Hence:
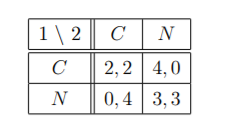
There is only one such NE in this subgame: both players play C in t=2, and play C the next stage is reached. The playersípayo§s are (2; 2).
Next, consider the subgame that equals the overall game. Since our goal is to Önd SPE of the overall game, we will be looking only for NE of this subgame in strategies that prescribe for the players to play (C; C) in the event that the second period is reached (i.e. if the players play (N; N) in t=1), and that prescribe for the players to play (C; C) in the event that the third period is reached. Hence:
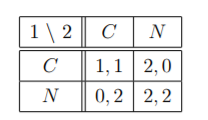
Hence there are two SPE of the overall game: ((C; C; C);(C; C; C)) and ((N; C; C);(N; C; C)).
 更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 经济Problem代写
更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 经济Problem代写




发表回复
要发表评论,您必须先登录。