Math 124B/215B – Assignment 1
澳洲网课代考推荐 Using separation of variables, write down the series expansion for the general solution to the damped wave equation
Instructions: Submit your assignment to Gradescope as you did for the practice assignment. Label your problems clearly, and remember to the select page number (or numbers) for each part of each problem which you upload to Gradescope. Your solutions will be graded for mathematical clarity and correctness. 澳洲网课代考推荐
(1) Using separation of variables, write down the series expansion for the general solution to the damped wave equation with Dirichlet boundary conditions
utt(x, t) + ut(x, t) − uxx(x, t) = 0, 0 < x < 1, −∞ < t < ∞
u(0, t) = u(1, t) = 0, −∞ < t < ∞.
(2) Find all nonzero solutions X(x), λ of the problem
− X 00(x) = λX(x), 0 ≤ x <≤ <a href="https://paperdaixie.com/澳洲网课代考推荐/">澳洲网课代考推荐</a>) = 0.
X(0) = 0, X0(
(3) Show that the problem
− X00(x) = λX(x), 0 < x < X(0) = 0, X0() + X(`) = 0
has no nonzero solutions X(x) when λ ≤ 0. (You don’t have to find any solutions.)
(4) Define the function
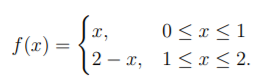
(a) Find the Fourier sine series expansion of f(x). You may use the formula
(b) Find the Fourier cosine series expansion of f(x). You may use the formula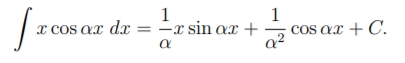

更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 澳洲数学网课代考




发表回复
要发表评论,您必须先登录。