MATH0051: Analysis 4 — Real Analysis
数学真实分析代写 Let (X, dX), (Y, dY ) and (Z, dZ) be metric spaces. Using the definition of continuity in terms of preimages of open sets, prove
Problem sheet 5 数学真实分析代写
Due 4pm Friday 19th February. Submit a single pdf file using the Moodle link.Compulsory questions are marked by ⇤. Some of them will be assessed.Non-compulsory questions include standard questions (⇧) and harder questions (†).
1.⇧ Let (X, d) be a metric space and x0 2 X. Define a mapping f : X ! R by f(x) =d(x, x0). Prove that f is continuous.
2.* Let F : C[0, 1] ! C[0, 1] be the map defined by (F(f))(x) = sin(f(x)). Show that F is continuous as a map from (C[0, 1], || · ||sup) to (C[0, 1], || · ||1). Hint: Use the mean value theorem for sin(t).
3.* Let `2 be the space of all square-summable real sequences x = (xn)n2N with the norm 数学真实分析代写
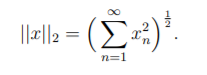
Let a 2 `2. Prove that
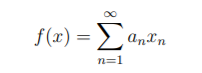
is well-defined for x 2 2 and defines a continuous function from (2, || · ||2) to R equipped with the standard metric.
4.* Consider the set of integers Z with the 2-adic metric 数学真实分析代写
![]()
if x 6= y and d(x, y) = 0 if x = y.
(a) Describe the open balls of radius 1 around the centres 0 and 1.
(b) Let f : Z ! R be defined as f(x) = 0 if x is even and f(x) = 1 if x is odd. Is f a continuous function from (Z, d) to R equipped with the standard metric?
Hint: Use the criterion of continuity in terms of open sets.
5.⇧ Let (X, dX), (Y, dY ) and (Z, dZ) be metric spaces. Using the definition of continuity in terms of preimages of open sets, prove that the composition g f : X ! Z of two continuous functions f : X ! Y and g : Y ! X is continuous.
6.⇧ Let f : R2 ! R be a continuous function with respect to the Euclidean metric in R2 and the standard metric in R. Suppose that f(x) > 0 for all ||x||2 > 1. Prove that the null set {x 2 R2 : f(x)=0} of f is compact. 数学真实分析代写
7.⇧ Consider the set N with the metric
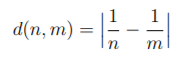
(a) Describe all convergent sequences in (N, d).
(b) Describe all continuous functions from (N, d) to the space R equipped with the standard metric.
Hint: You may find the sequential definition of continuity useful here (but some other methods will work too).
8.† Describe all continuous functions from R with the standard metric to R with the discrete metric. 数学真实分析代写





发表回复
要发表评论,您必须先登录。