MATH 142B Assignment 1B
Due: 11:59 pm pacific time on Friday, April 9
数学Assignment代写 It is important that the write-up of your solutions is your own. Directly copying or paraphrasing solutions from an external
Only complete this assignment if you have been assigned to Group B.
If you have been assigned to Group A, complete Assignment 1A instead. 数学Assignment代写
• Students are welcome to discuss assignment problems with their peers and to consult external written resources in completing assignments. However, students are
not permitted to use websites or webpages dedicated to posting solutions to homework/textbook problems (including posted solutions to homework problems from other courses).
It is important that the write-up of your solutions is your own. Directly copying or paraphrasing solutions from an external resource is plagiarism. To avoid this, always write up your solutions without external aids in front of you.
• If you use an external resource to help you complete an assignment problem, you must list this reference on your assignment.
• Students must submit their assignments through Gradescope, which can be accessed through Canvas.
– Instructions for how to use Gradescope are found at gradescope.com/help
– Submissions must be correctly oriented and easily readable.
• Late assignments will not be accepted.
Only complete this assignment if you have been assigned to Group B.
If you have been assigned to Group A, complete Assignment 1A instead. 数学Assignment代写
- Abbott Exercise 2.4.9.
- Fully justify your answers to the following problems.
(a) Abbott Exercise 2.7.2(a).
(b) Abbott Exercise 2.7.2(c).
(c) Abbott Exercise 2.7.2(e). (a) Abbott Exercise 2.7.4(a).
(b) Abbott Exercise 2.7.4(b).Consider the sequence {xn} where
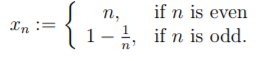
Determine lim sup xn and lim inf xn. Fully justify your answers.
5. Suppose {xn} is a bounded sequence and {xni} is a subsequence. Prove that
![]()
Remark. It can similarly be proven that![]()
- Suppose {xn} and {yn} are bounded sequences with xn ≥ 0 and yn ≥ 0 for every n ∈ N. Prove that
lim sup(xnyn) ≤ (lim sup xn) (lim sup yn).

更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 英文论文代写价格




发表回复
要发表评论,您必须先登录。