MAT401
Homework 4
代考数学quiz These problems are due on Crowdmark by 6pm on Wednesday, March 2nd. The solutions will be discussed in tutorials that week.
Read: Gallian, Chapter 18 (Omit the material on Euclidean domains) and Chapter 20, pp 338 –344.
You should also review Chapter 19, since we will assume this material on vector spaces is known.
Problems: 代考数学quiz
These problems are due on Crowdmark by 6pm on Wednesday, March 2nd. The solutions will be discussed in tutorials that week.
- Let R = Z[√−3]. Show that every element a ∈ R with a 6 = 0 and a not a unit is a product of irreducible elements. Note that we have seen that such a product is not unique.
- Suppose that R is an integral domain with the property that every strictly decreasing chain of ideals
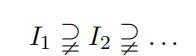
is fifinite. Show that R is a fifield.
- Let α be the real number 代考数学quiz
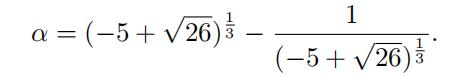
(i) Show that the fifield Q(α) ⊂ R is isomorphic to
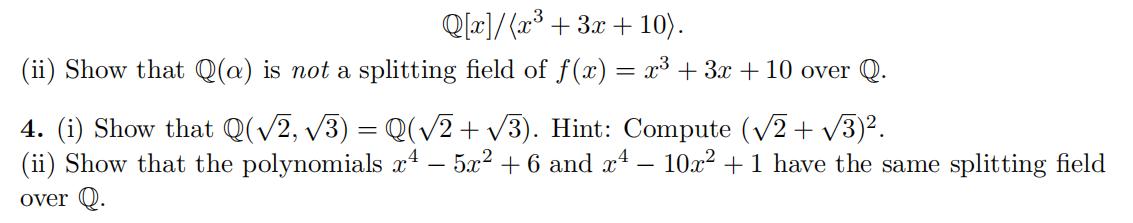





发表回复
要发表评论,您必须先登录。