STA 104 Winter Quarter, 2021
Sample Final Exam Solution
stat代写 Someone states “The larger the number of neighbors (i.e, the larger the value of K), the better the prediction. Do you think this is
True/False stat代写
For each of the following questions indicate true or false, then explain your answer. You may use examples to illustrate your answer.
(I) If we increase the number of random permutations, the permutation based p-value’s error decreases.
• Solution: TRUE. The larger the number of permutations, the closer our permutation distribution will be to all possible permutations.
(II) Classification trees always split on every X variable in the dataset.
• Solution: FALSE. If the variable did not improve the error rate, it would not be used in a split.
(III) If we conclude that we reject the null for an ANOVA test, we can immediately conclude that all group means are different.
• Solution: FALSE. We would need to use a permutation based cutoff to see which groups are different. It could be that only 1 group out of 3 is significantly different, for example.
(IV) The normal approximation to the binomial distribution requires a sample size larger than 30.
• Solution: FALSE. We need at least 5 observations above and below the hypothesized median.
(V) If a scatter plot for linear regression shows outliers, we should not use Spearman’s Rank correlation.
• Solution: FALSE. Spearman’s Rank correlation is not highly affected by outliers.
(VI) The larger the number of folds (the larger F) in cross fold validation, the more data we use to predict the part we “left out”.
• Solution: TRUE. If we leave out 1/20 of our data (K = 20), we are using 19/20 to predict 1/20, and if K = 2, we are using 1/2 of our data to predict the other half.
Full Detail stat代写
Work out the following problems. Show your work. No partial credit will be given without work shown, even if the answer is correct.
1. States are considering lowering the blood-alcohol level (BAL) at which drivers are considered to have a DUI. A group of subjects received a placebo (P), and a group received a specified amount of alcohol (A). The reaction time in seconds for a specific driving situation follows, along with the ranks:

Further, the overall variance in ranks is: 33.25 with an overall mean rank of: 10.5. Consider the claim to be that there was significant impairment (increased reaction time) in group A.
(a) State the null and alternative in terms of the CDF.
• Solution: Let group P be group 1, and group A be group 2.
H0 : F1(X) = F2(X) vs. HA : F1(X) ≥ F2(X)
(b) Using the large-sample approximation to Wilcoxon Rank Sum, find the test-statistic and the p-value.
• Solution: The sums of the ranks for both groups are: Group P: 70, Group A: 140.Thus, if we use Group![]() , with corresponding p-value P(Z < −2.65) ≈ 0.004 If we use Group
, with corresponding p-value P(Z < −2.65) ≈ 0.004 If we use Group![]() with corresponding p-value P(Z > −2.65) ≈ 0.004
with corresponding p-value P(Z > −2.65) ≈ 0.004
(c) Do you think there was significant impairment? Justify your answer.
• Solution: Yes. Since the p-value for the hypothesis is very small, we reject the null and conclude that the average reaction time is longer for group A than B.
(d) What about this dataset suggests that a non-parametric test may be more appropriate than a parametric test? Explain.
• Solution: There is a small sample size for each group, so a parametric tests’ assumptions are violated.
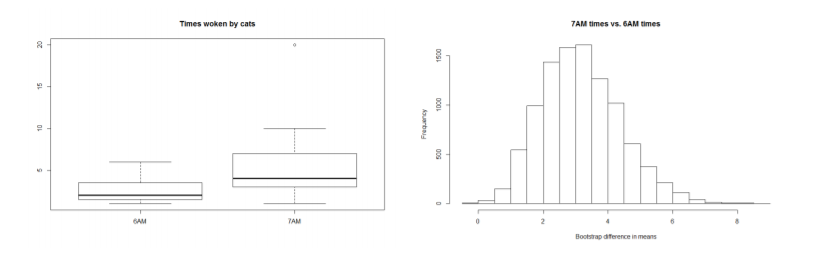
2. A frustrated instructor measures the number of times their cat wakes them up before the alarm goes off when they the alarm set for 6AM, or 7AM. The boxplot of the number of times they were woken up, and the bootstrap distribution for the difference in means follows: stat代写

The observed difference in means (7AM vs. 6AM) was : 3.167. stat代写
(a) What other bootstrap estimates may be useful in determining what type of bootstrap confidence interval we should use? Explain.
• Solution: The bias - if there is significant bias, we should use a BCA interval which will correct for that bias.
(b) The percentile confidence interval is: (1.329, 5.325). Interpret the confidence interval in terms of the problem.
• Solution: We are 90% confident that the average number of times the owner was woken up at 7AM is larger than that at 6AM by between 1.329 and 5.325.
(c) Explain how a bootstrap percentile confidence interval was found in this problem.
• Solution: We find the 5th and 95th percentile of the bootstrap distribution of the
(d) What type of confidence interval (BCA or percentile) would you use for this data, and why?
• Solution: BCA - there are outliers, and significant skew to the bootstrap distribution of θ.
3. The amount of money that a certain type of worker spends on health care in one year for 20 workers is shown below (in dollars): 143, 172, 197, 201, 208, 218, 219, 223, 248, 254, 276, 326, 342, 345, 398, 400, 531, 1290, 3142, 4321
(a) Find the 95% confidence interval for the median, using the normal approximation to the binomial distribution.
• Solution: To find the lower bound, we use the value in the![]() position, rounded to the nearest integer. I.e, the 1.96
position, rounded to the nearest integer. I.e, the 1.96![]() value, which is 218. To find the upper bound, we use the value in the
value, which is 218. To find the upper bound, we use the value in the![]() position, rounded to the nearest integer. I.e, the 1.96
position, rounded to the nearest integer. I.e, the 1.96![]() value, which is 398. Thus the confidence interval is: (218, 398)
value, which is 398. Thus the confidence interval is: (218, 398)
(b) Does your confidence interval support the claim that workers spend over $400 a year on health care? Explain.
• Solution: No, since the confidence interval is not strictly over 400, it does not support this claim.
(c) Do you believe a parametric confidence interval for the mean would be appropriate in this case? Why or why not.
• Solution: No - there are significant outliers in the dataset, and the sample size is below 30.
(d) What is the largest value we expect the median amount that workers spend on health care in one year to be? Explain your reasoning.
• Solution: Based on our confidence interval, 398.
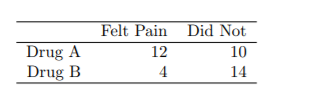
4. A new drug (Drug B) was being tested on how long it numbed limbs (arms or legs), compared to an old drug (Drug A). An hour after the drug was administered, the limbs were tested, and the subjects reported if they felt pain or not.
The results are: stat代写
Assume the observed value of the test-statistic is:![]()
(a) State the null and alternative for comparing the probability of feeling pain conditional on drug type.
• Solution: H0 : P(F eltP ain|DrugA) = P(F eltP ain|DrugB) vs H0 : P(Numb|DrugA) 6= P(Numb|DrugB)
(b) If the distribution of 10000 permutation test-statistics is:

Estimate the p-value. Would this p-value be the same if we ran another 10000 random permutations?
• Solution: The estimated p-value is between 0.022 and 0.053. No - the p-value range may change since it is based on random permutations.
(c) State the conclusion in terms of the problem if α = 0.10.
• Solution: We fail to reject the null and conclude there is a different in the probability that the limb remained numb for Drug A and Drug B.
(d) Which drug was more effective in keeping the limb numb? Explain.
• Solution: Since![]() drug B was more successful in keeping the limb numb.
drug B was more successful in keeping the limb numb.
5. KNN was used to predict if someone was “obese” or not, based on Age, average number of “sitting” minutes per day, systolic blood pressure, and height. The misclassification rate for various F folds and K neighbors follow: stat代写
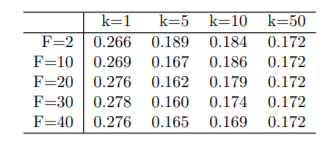
(a) Which combination resulted in the highest misclassification rate? Why do you think that is?
• Solution: F = 40 and K = 1. Choosing 1 neighbor is highly variable, and the predictions would often change.
(b) Someone states “The larger the number of neighbors (i.e, the larger the value of K), the better the prediction. Do you think this is true? Explain your answer.
• Solution: This is not true. For example, the largest value of K is choosing the entire dataset as a “neighbor”, which would be a very vague prediction.
(c) The error matrix for the “best“ K and N is:

What is a potential issue with our predictions based on the above? Explain.
• Solution: We only predicted one person as Obese. The error rate for predicting someone as Obese is very large.
(d) What would you predict the probability of someone being obese was, if K = n? Explain.
• Solution: 71/(341 + 1 + 71) = 71/413 = 0.1719. We would use the overall proportion of people who were obese, since we are using every observation.

更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 数据库作业代写




发表回复
要发表评论,您必须先登录。