数学专业Homework代写 MAT 127C: Real Analysis Homework 9

MAT 127C: Real Analysis
Homework 9

数学专业Homework代写 his problem set is due Friday, May 29, by 9pm Pacific time in Gradescope. Brief reminders: Please write each solution on

This problem set is due Friday, May 29, by 9pm Pacific time in Gradescope. Brief reminders: Please write each solution on separate pages. Please list all main study partners on the first page of your homework. You should have justification in complete sentences for all questions, even those that are mainly calculation.

Note: Homework problems in this class are not to be posted online until after the end of the quarter.

9.1. Define f : R2 → R by 数学专业Homework代写

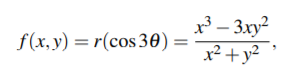
and f(0,0) = 0. Prove that f is Lipschitz. (Note and hint: This is the same function as problem 5.1(a) and in lecture for a different purpose. f is not a C1 function, but you can follow the proof from lecture that C1 functions on bricks are Lipschitz. Namely, if the derivative of f is bounded, you can integrate the derivative you can show that its derivative is bounded and integrate it. The origin is a special case because f is not differentiable there; although it does have directional derivatives.)

9.2. Define a region U 2 ⊆ R2 that consists of two particular open squares:

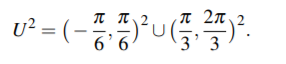
Also define a map ~g : U2 → R2 as follows

The goal of this problem is to understand ~g as a change of variables on U2 数学专业Homework代写

(a) Draw (s,t) coordinates in the region U2 the (x, y) plane as you did in problem 8.1. Draw a pair of coordinate directional vectors ∂/∂ s and ∂/∂t at least one point (x, y) in each of the open squares of U 2 . (Note: You can use graphing software such as the excellent Desmos to help you. However, if it does not label everything that you want, you should print it out or copy it to add labels somehow, or add explanation to make a complete answer. Also, if using color, please make the curves with constant s one color and the curves with constant t a second color.

(b) Prove that ~g is a C1 diffeomorphism from U2 to its image V2 =~g(U2). (Note: It is a bit tricky to prove that ~g is one-to-one onto its image. You can either give a computational proof; or for this part of the question, you can give an informal argument referring to your answer in part (a).) (c) Find orientations of U2 and V2 to make ~g an oriented diffeomorphism from U~ 2to ~V2

更多代写： HomeWork cs作业     金融代考    postgreSQL代写         IT assignment代写     统计代写    计算机科学Homework代写