exam daikao_数学484考试代写：Math 484 Fall Exam

Math 484 Fall Exam

数学484考试代写 Solve the (primal) LP from (1) by pivoting in Mathematica according to the simplex algorithm using Bland’s Rule with the

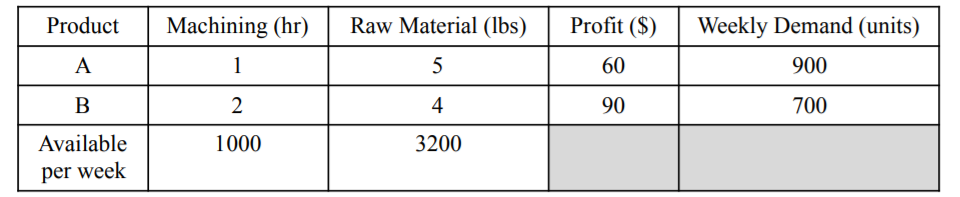
A company manufactures two products, A and B. The company forecasts demand to avoid producing more than they
can sell. The manufacture of each product requires raw material and machining.

The table summarizes the per unit consumption of the raw material and machining for each product, along with the profit and weekly demand. Assume no negative production and profit includes all costs except any extra raw material and/or machining time purchased.

1. Write an LP to determine how many of each product should the company make to maximize profit. Use Mathematica comments to document it at the top of your file.

1. Using Mathematica, graph the feasible set. Use Mathematica’s drawing tools to add any constraint that cannot be plotted as a function. Mark feasible set and solution point in your graph using drawing tools such as text box and circle.




2. Solve the (primal) LP from (1) by pivoting in Mathematica according to the simplex algorithm using Bland’s Rule with the “natural ordering” (i.e. control variables 1,…,n then slack variables 1,…,k) … Document the optimal production plan and corresponding profit in a text box on your plot.  数学484考试代写




3. If no more machining time is available, but more raw materials can be bought at $4/lb., should the company buy more? If so, how much more? Answer this question graphically and make a new plot to show the answer. Then make a new tableau, using the new value of b2 and including as a constant in the objective the price of any resources bought or sold. Pivot to the new solution by the simplex algorithm, and document the new production plan and optimal profit in the plot as in (3). Be sure to find all optimal tableaux for use in question (5).

5. Copy and paste your plot from (4) so you have a working copy to explore changing constraints. Use this plot and
your optimal tableaux from (4) to answer the questions that follow, and document your answers in a Mathematica comment. Starting at the solution to (4), ignoring the price of resources, what is the change of z*  数学484考试代写

i. per unit increase in machining? (holding all other variables constant)
ii. per unit decrease in machining? (holding all other variables constant)
iii. per unit increase in raw materials? (holding all other variables constant)
iv. per unit decrease in raw materials? (holding all other variables constant)v. per unit increase in demand for product A? (holding all other variables constant)
vi. per unit decrease in demand for product A? (holding all other variables constant)
vii. per unit increase in demand for product B? (holding all other variables constant)
viii. per unit decrease in demand for product B? (holding all other variables constant)  数学484考试代写

1. Starting at the solution to (4), if more machining time can be purchased for $28/hr and more raw material can be purchased for $4/lb., should either or both be purchased and, if so, how much of each should be purchased if the company has $34,800/week to invest? Formulate and solve a new LP in Mathematica with additional variables for resources purchased, and document the optimal resource purchase, production plan and net profit in a new plot (still in x1-x2 space) and mark x1,x2. (Resource purchases x3*, x4* in text only - not shown in plot.)

商科代写 cs代写 法律学代写 经济学代考_经济学作业代写 艺术代写 心理学代写  哲学代写 伦理学代写 体育学代写 化学代写 教育学代写 医学代写 历史代写