MATH 3330: Applied Graph Theory
Fall 2020
Course Description: (from calendar)
Math数学网课代考 Become familiar with the basic concepts concerning graphs, such as vertex, edge, degree, connectivity, path, tree, etc.
This course offers an introduction to graph theory, with an emphasis on applications and modelling. Topics include: paths and cycles, shortest route problem, connectivity and trees, minimum spanning trees, network flow, planar graphs, matchings, assignment problem, graph colouring and applicationsto scheduling, Hamilton cycles, and the Travelling Salesman Problem Prerequisites: MATH/CSCI 2112 or MATH 1030.
Instructor: Jeannette Janssen
Email: Jeannette.Janssen@dal.ca
Office hours: TBA. Help will also be available through the Discussion
Board in Brightspace.
Delivery: Math数学网课代考
There will be one synchronous lecture per week, usually on Monday 9:35–10:25, via Collaborate Ultra in Brightspace. Attendance is mandatory. However, lectures will be recorded for those that are unable to attend at the appointed time. In addition, short instructional videos and notes will be posted on Brightspace.
Course Text:
Graph Theory and its Applications, J.L. Gross, J. Yellen, M. Anderson, 2018, Chapman Hall/CRC, Third Edition, ISBN 9780429425134. The book is mandatory, and readings from the text will constitute an important part of the course. The book is available from the Dalhousie bookstore. An e-book is available from the publisher here; this includes an option to rent the text at half price. Note: earlier editions of this text are also acceptable. Math数学网课代考
Evaluation and course policy:
Assignments. There will be biweekly long-form assignments. These must be typed or handwritten, converted to a pdf file, and submitted via Brightspace. Please follow the exact instructions regarding formatting and submission, to facilitate marking. While you are encouraged to work together with your class mates, the final write-up of the assignment must be done individually; please read the university plagiarism policy, that can be found on the course Web page. Any material consulted must be properly credited; this includes web pages, or personal communication.
Late assignments will be penalized by 5% for up to 12 hours late, 10% for 12–24 hours late. Assignments more than 24 hours late will not be accepted. There will be one make-up assignment in due on the last day of classes; students that missed an assignment for a valid reason may use this assignment to replace the missing mark. No make-up possibilities for more than one missed assignment. Please use the Student Declaration of Absence form.
Quizzes. Math数学网课代考
There will be five quizzes during the term. These will be held on Sept. 25, Oct. 9, Oct. 26, Nov. 16, and Nov. 30. The quizzes will be open for 60 minutes, in a time interval of 90 minutes. Time of day will be determined later, in such a way that students in different time zones will be accommodated. Students missing one quiz for a valid reason will be given the opportunity to take a make-up quiz near the end of term. No make-up opportunity is possible for students missing more than one quiz. Quizzes should be done individually, and be held while adhering to academic integrity guidelines. Any breach of these guidelines will be brought to an academic integrity officer. In particular, no use may be made of “tutoring” help sites (Chegg, CourseHero). If I find evidence of a quiz or assignment question on one of these sites, the question
will be considered compromised, and discounted for everyone in the class.
Group project.
This will be done in groups of 3 students. Groups will read and discuss a scientific paper on an application of graph theory (chosen from a given list). Groups will prepare an infographic, comment on submissions of other groups, and answer questions in an oral evaluation session.

Conversion of numerical grades to Final Letter Grades follows the Dalhousie Common Grade Scale:
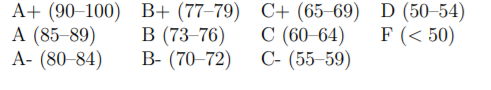
Topics: Math数学网课代考
Paths, cycles and the concept of diameter: are all humans really connected by at most ”six degrees of separation”?
Shortest paths: What is the shortest way of routing packets through the Internet?
Connectivity, strong connectivity, connected components: communities in social networks
Connectivity and spanning trees: what is the minimum cost, or maximum reliability network needed to connect a set of servers?
Minimum flow and maximum cut: how scheduling problems can be solved efficiently using graph theory
Graph models: how graphs are used to model real-life networks such as ecological networks, the World Wide Web, the Internet, biological networks, and social networks.
Learning objectives:
Become familiar with the basic concepts concerning graphs, such as vertex, edge, degree, connectivity, path, tree, etc.
Become familiar with basic concepts and parameters of network science and other applications of graphs, such as degree distribution, clustering, centrality, network flow, etc.
Be able to do elementary proofs (logical arguments) in graph theory
Be able to determine the value of simple graph parameters (such as connectivity, diameter,..) for a specific given graph
Be able to understand and execute the algorithms to compute graph optimization parameters such as minimum spanning tree and shortest path.
Be able to understand and summarize a paper in the social or physical sciences where graph theory/network science is used in the study of a real-world topic.
Be able to model a ”real-world” problem as a graph problem. Math数学网课代考





发表回复
要发表评论,您必须先登录。