MAT401
Homework 9
mathHomework代写 These problems are due on Crowdmark by 6pm on Wednesday, March 30th. The solutions will be discussed in tutorials that week.
Read: Gallian, Chapter 32 and the Notes on Fields Extensions.
Problems: mathHomework代写
These problems are due on Crowdmark by 6pm on Wednesday, March 30th. The solutions will be discussed in tutorials that week.
- Find a Galois extension E/Q of degree 11.
- Show that the polynomial
is not solvable by radicals. - Suppose that E is the splitting fifield over Q of the polynomial
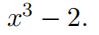
- Q. Thus the are(i) Show that the polynomial x2 − 5 is irreducible in E[x].Hint: Otherwise, there would be a root β ∈ E of this polynomial and a subfifield Q(β) in E.
Now apply Galois theory.
(ii) Let K = E(√ 5). Show that K is a Galois extension of Q with |K : Q| = 12.
(iii) Show that G = Gal(K/Q)' Z2× S3.Hint: K has subfifields E and F =Q(√ 5) which are Galois extensions of restriction maps
- Q. Thus the are(i) Show that the polynomial x2 − 5 is irreducible in E[x].Hint: Otherwise, there would be a root β ∈ E of this polynomial and a subfifield Q(β) in E.
rE : G −→ Gal(E/Q) and rF : G −→ Gal(F/Q). mathHomework代写
Show that the map
G −→ Gal(E/Q) × Gal(F/Q), σ 7→ (rE(σ), rF (σ))
is an isomorphism.
(iv) Let η =√ 5 +3√2 ∈ K and let L = Q(η) be the subfifield it generates.
Determine
Gal(K/L) = {σ ∈ Gal(K/Q) | σ|L = idL}
and |L : Q|.
- Suppose that G is a solvable group and that C is a subgroup. Prove that C is solvable. mathHomework代写
发表回复
要发表评论，您必须先登录。