MAT 128A Midterm Exam
Mathematics Admissions Test作业代写 If you use the Lagrange polynomial of order 5, will the approximation be more accurate assuming all
Your exam’s work should come from your own work. Sharing codes/answers or Posting the questions on Chegg violates the UC Davis Honor Code, and I will be thoroughly checking Chegg for any posts relating to this exam.
Due: Friday 8/28 at 11:59 pm on Gradescope. Late submision window is upto Monday 8/31 at 11:59pm with 10 points
late pelnalty.
Problem 1 ( 20 points): A car traveling along a straight road is clocked at a number of points. The data from the observations are given in the following table, where the time is in seconds, the distance is in feet, and the speed is in feet per second.
a/ Use a Hermite polynomial to predict the position of the car and its speed when t = 10 s.
b/ Use the derivative of the Hermite polynomial to determinethe first time the car exceeds 55 mi/h speed limit on the road.
c/ What is the predicted maximum speed for the car?
d/ Besides Hermite interpolations, what are other methods that you learn in Mat128A can be applied in part b/?
Problem 2 ( 20 points): The number 5 is drawn by the following 21-piece Bézier curve and is shown in the below graph.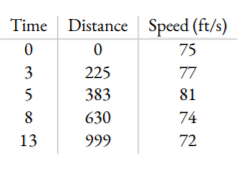

a/ Use a data digitizer (Engauge Digitizer is recommended) to get all of the spline/end point coordinates into an Excel sheet, which allows to copy them into Python.
b/ Provide the plot of the Bezier curves. You may use the data data digitizer to scan in your coordinates for the control points. For each Bézier curve that is a straight line segents (0 − 1, 2 − 3, 3 − 4, 5 − 6, 6 − 7, 7 − 8, 20 − 0), you choose the controls points to be the end points. For other curves, choose the control points as shown in the following figure:
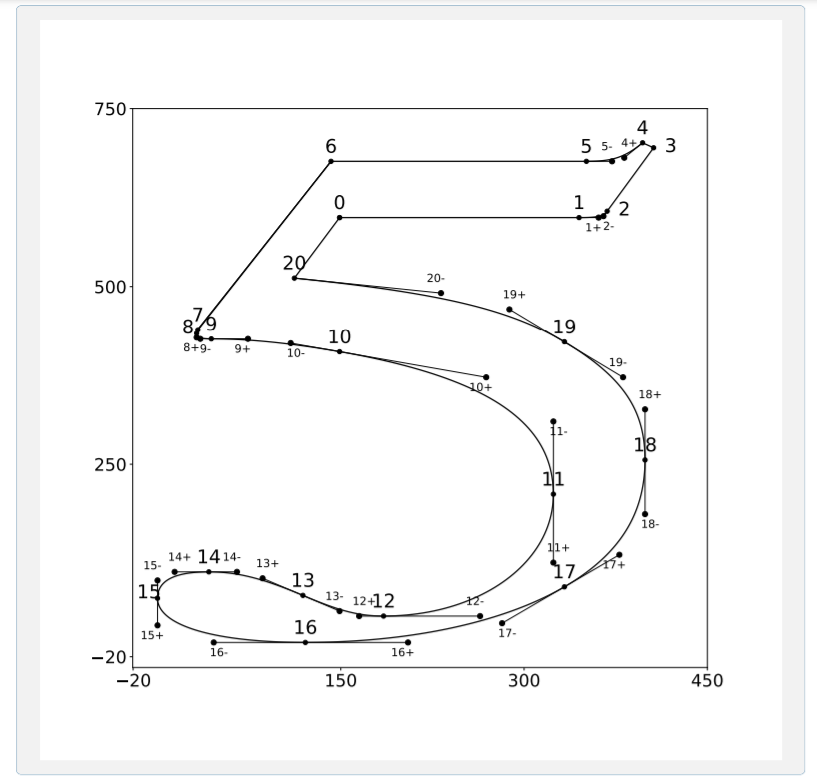
The graphs of these two figures are provided in pdf form in the ‘midterm’ folder. You can import them into Engauge digitizer directly or after transforming them into pgn of jpeg files depending on the version of your Engauge Digitizer. Mathematics Admissions Test作业代写
❖ Import the picture into Engauge Digitizer. Make sure to choose the option ‘with points only’, that means do not choose ‘with lines (with or without points).
❖ Add first of three axis points, which you should click and enter the coordinate of the points(−20, 750),(−20, −20),(450, −20)
❖ Next click ont 21 points of the end points
❖ Ignore the any curve showing on screen and click Export and name your file, say e.g. plot.cvs
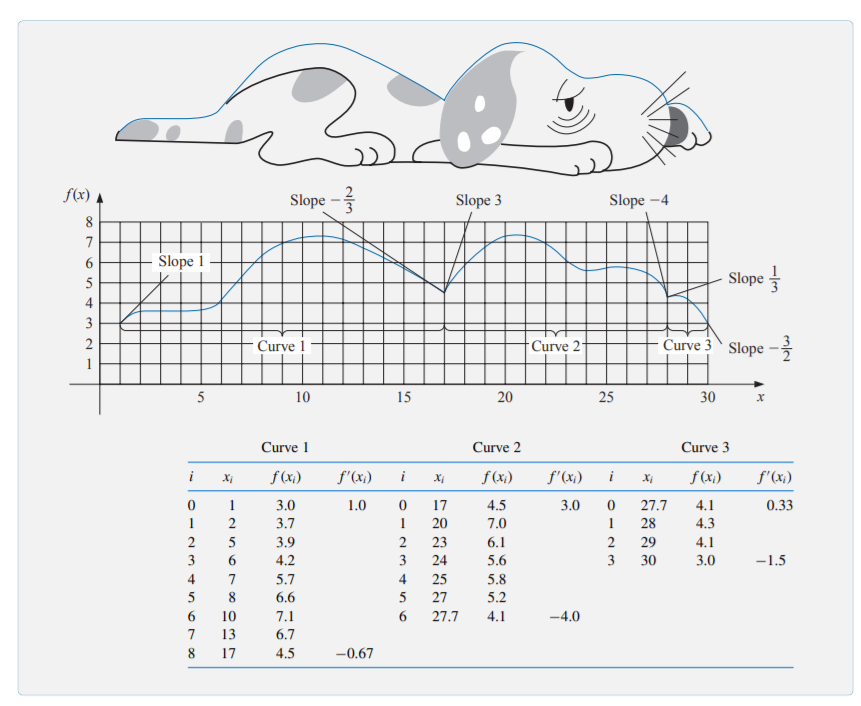
❖ You can open the plot.cvs by Excel, or Panda and import directly into Python. Problem 3 ( 20 points): The upper portion of this noble beast is to be approximated using clamped cubic spline interpolants. The curve is drawn on a grid from which the table is constructed. Construct the three clamped cubic splines.
Problem 4 ( 20 points): Consider the data table below to find the following values using appropriate choice of Newton divided difference formulas Mathematics Admissions Test作业代写

Problem 5 ( 20 points): The population of the US in thousands is given below
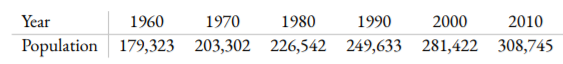
a/ Find the population at 1985 using this data table and the first order Lagrange polynomial interpolation.
b/ If you use the Lagrange polynomial of order 5, will the approximation be more accurate assuming all derivatives of the function for the data table is bounded by 1? Explain.

更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 statistics代写




发表回复
要发表评论,您必须先登录。