计算机Exam代考 CAS MET 582 Exam II

CAS MET 582 Exam II

计算机Exam代考 Justify your solutions fully as indicated in lecture for fullest credit. Each of the 5 problems counts 20%. (50 minutes total for

Instructions:  计算机Exam代考

Justify your solutions fully as indicated in lecture for fullest credit. Each of the 5 problems counts 20%. (50 minutes total for this exam; this exam is a little on the long side so prioritize problems that you feel comfortable working!)

1. Suppose in a certain parametric family, it happens that = E[log(X)], where X>0 is non-degenerate. Propose an estimator, call it n^ , for  and then prove that your estimator is UCAN. (Hint: Use the “Golden Rule.”) Tell us briefly how to compute the asymptotic normal variance if the distribution of X is known.

2.. Let Yn have chi-squared distribution with n df. Find the asymptotic distribution of

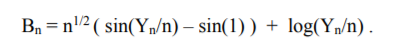
Hint: start with a CLT for Yn/n by viewing it as a sample mean of suitable rv’s.

1. Consider a finite set of strictly positive numbers not all of which are the same, although some repeats might occur. Show rigorously that the exponential of the
   mean of the logs of the numbers, is always strictly less than the arithmetic mean of those original numbers. Justify your work.




2. Let X ~  (5, 3) (note E(X) = 5/3 here). Compute E[ 1/X ] exactly. Show all your work.




3. Consider the family Exp(),  > 0. (Recall here  is the constant failure rate.) Find Fisher’s information function I() for this family Exp(),  > 0. Find MLE(); show your estimator is CAN for  but show your estimator is biased for  Find Fisher’s information function I() for this family Exp(),  > 0.

更多代写： HomeWork cs作业     金融代考    postgreSQL代写         IT assignment代写     统计代写  雅思可以找枪手吗