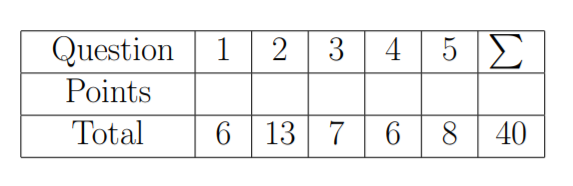
Linear and non-linear ODEs, Math 134
Exam 3
英国数学代考 such that the origin is a Lyapunov stable but not attracting fixed point? If yes, please provide an example and draw the phase
Important information regarding the exam: 英国数学代考
(a) You have 24 hours to upload your solutions; from Thursday, July 29, 9am (PDT) to Friday, July 30, 9am (PDT).
(b) The exam is open book; you may also use online sources. Calculators, including wolfram alpha, are allowed.
(c) You are required to follow the student conduct code, which is available at www.deanofstudents.ucla.edu. In particular, you are not allowed to receive assistance of any kind from any other person while working on the exam.
(d) Please acknowledge the honor code by completing the corresponding survey on ccle. You must acknowledge and follow the honor code to receive credit for the exam. It is sufficient to complete the survey once (for the entire quarter).
(e) You must show your work to receive full credit, unless stated explicitly otherwise.
(f) Please write your full name and your UID on the front page of your exam.
Good luck!
Exercise 1 (3+3 points) 英国数学代考
(a) Is there a 2-dimensional ODE system
x˙ =
y˙ =
such that the origin is a Lyapunov stable but not attracting fixed point? If yes, please provide an example and draw the phase portrait. If not, please explain why.
(b) Is there a 2-dimensional ODE system
x˙ =
y˙ =
with a closed orbit and single fixed point, which is a saddle point?
If yes, please provide an example and draw the phase portrait. If not, please explain why.
Exercise 2 (1+3+6+3 points)
Consider the differential equation
x¨ = x 2 − 11x + 10
(a) Write the differential equation as a first order ODE system.
(b) Calculate all fixed points and classify them using linear stability analysis.
(c) Find a conserved quantity for the differential equation. Show that your quantity is indeed preserved. Classify the fixed points of the non-linear ODE.
(d) Draw a plausible phase portrait. Indicate the stable and unstable manifolds.
Exercise 3 (7 points)
Show that the differential equation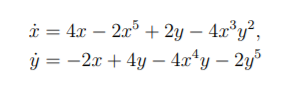
has a closed orbit. You may use that the origin is the only fixed point.
Exercise 4 (6 points)
Use the function
L(x, y) = x n + ay2,
for appropriate choices of a > 0 and n ∈ N, to show that the origin is the unique fixed point of the differential equation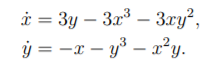
Deduce the stability type of the origin.
Exercise 5 (4+4 points) 英国数学代考
For µ ∈ R consider the differential equation
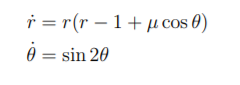
(a) Draw the phase portrait for µ = 0. Remark. You do not need to compute the linearization at the fixed points.
(b) Is there a closed orbit that encloses the origin? Please explain.





发表回复
要发表评论,您必须先登录。