英国作业代写_多元数据分析方法在物流业中的应用

The Application of Multivariate Data Analysis Methods in Logistic Industry

多元数据分析方法在物流业中的应用

英国作业代写  Under this section the scholarly journals on the application of Multivariate Data Analysis Methods in logistics industry will be..

Literature Review

Under this section the scholarly journals on the application of Multivariate Data Analysis Methods in logistics industry will be reviewed. Particularly the main aim of the Multivariate Data Analysis Methods was exploration, classification, and value forecasting. There are different multivariate data analysis methods in literature.

This paper only concentrates on those methods applicable to the applied marketing research in logistic industry. Therefore the review will not be exhaustive on the multivariate data analysis methods. The most popular methods in the applied marketing research are factor analysis and cluster analysis which will be used i the reviewed journals articles.

译文：文献评论  英国作业代写 

本节将回顾多变量数据分析方法在物流行业应用的学术期刊。 特别是多元数据分析方法的主要目标是探索、分类和价值预测。 文献中有不同的多元数据分析方法。

本文只关注那些适用于物流行业应用营销研究的方法。 因此，对多元数据分析方法的审查不会详尽无遗。 应用营销研究中最流行的方法是因子分析和聚类分析，它们将用于已审查的期刊文章。

Factor Analysis

Among the multivariate techniques molded here for review, factor analysis is most widely known and used by marketing practitioners and researchers.
Factor analysis is basically a method for reducing a set of data into a more compact form while throwing certain properties of the data into bold relief” (Anderson, T. W. 1958). More technically, it is a set of methods in which the observable or manifest responses of individuals on a set of variables are represented as functions of a small number of latent variables called factors.

It is, therefore, an attempt to descry those hidden underlying factors which have generated the dependence or variation in the responses. Such functions can be both linear and nonlinear although everyone generally limits himself to a linear functional relationship between the factors and the manifest responses (McDonald, 1962). A factor, then, is a linear combination of the variables in a data matrix. In other

译文：因子分析  英国作业代写 

在此处用于审查的多变量技术中，因子分析最为广为人知并被营销从业人员和研究人员使用。
因子分析基本上是一种将一组数据简化为更紧凑形式的方法，同时将数据的某些属性放入大胆的浮雕中”（Anderson，T. W. 1958）。 从技术上讲，它是一组方法，其中个体对一组变量的可观察或明显反应被表示为少量称为因子的潜在变量的函数。

因此，它试图描述在响应中产生依赖性或变化的那些隐藏的潜在因素。 这些函数既可以是线性的，也可以是非线性的，尽管每个人通常都将自己限制在因素和明显响应之间的线性函数关系中（McDonald，1962）。 那么，因子是数据矩阵中变量的线性组合。 其他

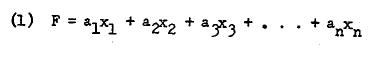
words,

Linear combinations are derived by using several judgmental criteria or the analytical criterion of least squares principle. The latter suggests a close resemblance to regression. However, the peculiarity of factor analysis lies in the fact that a number of linear combinations each giving one factor is more common. In short, it is not at all unusual to obtain a small number of factors in any data analysis. Thus, we can more generally stat, as follows:

译文：字，

线性组合是通过使用几个判断标准或最小二乘原理的分析标准得出的。 后者表明与回归非常相似。 然而，因子分析的特殊性在于，多个线性组合每个给出一个因子更为常见。 简而言之，在任何数据分析中获得少量因素并不罕见。 因此，我们可以更一般地统计，如下：

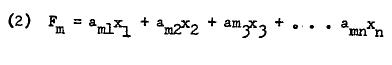
In factor analyzing a data matrix, two sets of values are obtained which are known as factor scores and factor loadings.4 A factor score is individual’s score as a result of linear combination of his manifest scores. Thus,

在对数据矩阵进行因子分析时，会获得两组值，称为因子得分和因子载荷。 4 因子得分是个人得分的线性组合，是其明显得分的线性组合。 因此，

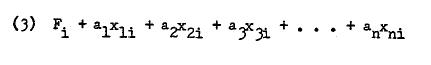
Since there are as many scores per individual i as there are linear combinations (factors), we may generalize (Banks, S. 1968) to this:

由于每个个体 i 的分数与线性组合（因子）一样多，我们可以将（Banks, S. 1968）概括为：

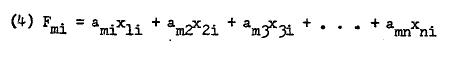
A factor loading is the correlation between factor scores and the manifest scores of the individuals in the sample.

These correlations may be high or low, positive or negative, depending on the dependence of manifest variables and the particular method of factor analysis. We may describe a factor loading as

译文：因子载荷是因子得分与样本中个体的明显得分之间的相关性。 英国作业代写 

这些相关性可能高或低、正或负，取决于明显变量的依赖性和因子分析的特定方法。 我们可以将因子载荷描述为

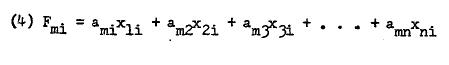
Factor analysis is more appropriately a set of data reduction techniques rather than a single unique method. Much of the confusion in marketing literature stems from not appreciating this fact. The set is created as a result of a variety of options available to the researcher for analyzing data. These options can be grouped as with regard to (Anderson, T. W. 1958) nature of data matrix to be factored,

Attneave, F. (1950) weights or coefficients to be specified in making the linear combinations, and (Banks, S. 1968) derivation of new (rotated) factors by transformation of original factors.

The option related to data matrix is with regard to factoring either a correlation matrix, a covariance matrix, or a cross—products matrix. Any multivariate analysis begins with a data matrix X consisting of n rows representing variables and N columns representing individuals. .n some cases, it is advantageous to redefine rows and columns by transposing the data matrix.

译文：因子分析更恰当地是一组数据简化技术，而不是一种独特的方法。 营销文献中的大部分困惑源于没有意识到这一事实。 该集合是由于研究人员可用于分析数据的各种选项而创建的。 这些选项可以根据要分解的数据矩阵的性质 (Anderson, T. W. 1958) 进行分组，

Attneave, F. (1950) 在进行线性组合时要指定权重或系数，以及 (Banks, S. 1968) 通过转换原始因子来推导新的（旋转的）因子。

与数据矩阵相关的选项是关于分解相关矩阵、协方差矩阵或叉积矩阵。 任何多变量分析都从一个数据矩阵 X 开始，该矩阵 X 由表示变量的 n 行和表示个体的 N 列组成。 在某些情况下，通过转置数据矩阵来重新定义行和列是有利的。

The cell xji refers to i individual’s response on jth variable.

This data matrix contains three types of information: level, dispersion and shape of variables or individuals. In some analyses, ail the three types of information are relevant. In that case, we obtain a cross—products matrix XX by post—multiplying the data matrix with its transpose. Each cell element contains sums of squares or cross products.

If only dispersion and shape are important, we may at first set levels of all variables equal, preferably at zero level, aid obtain transformed coil values which are deviation scores. A cross—products matrix of deviation scores becomes a covariance matrix when each cell is divided by the number of variables. Finally, if both levels aid dispersion are not relevant to the analysis we may equate both of these across the variables.

One way is to obtain standard scores where, means are equal to zero and variances are ail equal to unity. The cross—products of a matrix of standard scores then results in the well-known and common correlation matrix.

Obviously, covariance and correlation matrices are one specific way of removing the effects of level and dispersion on the data. They are commonly used because of their mathematical relationships to known distributions such as normal distribution. However, any other method of equalizing level aid dispersion would be relevant as data input for factor analysis.

译文：单元格 xji 是指 i 个个体对第 j 个变量的响应。  英国作业代写 

该数据矩阵包含三类信息：变量或个体的水平、离散度和形状。在某些分析中，所有三种类型的信息都是相关的。在这种情况下，我们通过将数据矩阵与其转置相乘得到一个叉积矩阵 XX。每个单元格元素包含平方和或叉积。

如果只有色散和形状很重要，我们可以首先将所有变量的水平设置为相等，最好是在零水平，以帮助获得作为偏差分数的转换线圈值。当每个单元格除以变量数时，偏差分数的叉积矩阵变为协方差矩阵。最后，如果两个级别的辅助分散都与分析无关，我们可以在变量中将这两个级别等同起来。

一种方法是获得标准分数，其中均值等于 0，方差都等于 1。标准分数矩阵的叉积然后产生众所周知的常见相关矩阵。

显然，协方差和相关矩阵是消除水平和离散对数据影响的一种特定方式。它们之所以常用，是因为它们与已知分布（如正态分布）的数学关系。然而，任何其他均衡水平援助分散的方法都与因子分析的数据输入相关。

Of course, there are some situations where a particular type of data matrix is almost mandatory.

For example, when the units of measurement of variables are quite diverse so as to lack common dimensionality, it is desired that data be standardized. On the other hand, if the researcher believes, based on his theory, that he should expect individual differences in the sample on level aid dispersion, it is better to use the cross—products matrix (Ross, 1964).

Finally, there are six separate ways that data can be correlated with the use of cross—products, covariance or correlation procedures because, in general, we have three kinds of information:

variables, people, and separate time periods. Holding one dimension Constant, and using the second dimension as replications, a cross— products, covariance or correlation matrix can be obtained on the various elements of the third dimension. For example, we may get a variable—by-variable correlation matrix, or people—by-people correlation matrix or time-by-time correlation matrix.

Cattell (1952) has given various labels to the six types out of which factoring a variable by variable at a point in time correlation matrix is called K—type factor analysis, and that of a person—by—person correlation matrix at a point in time is called Q—type factor analysis.

译文：当然，在某些情况下，特定类型的数据矩阵几乎是强制性的。

例如，当变量的计量单位非常多样，缺乏共同的维度时，就希望数据标准化。另一方面，如果研究人员认为，根据他的理论，他应该预期样本中的个体差异会导致水平辅助分散，那么最好使用交叉乘积矩阵（Ross，1964）。

最后，有六种不同的方法可以使数据与交叉积、协方差或相关程序的使用相关联，因为一般来说，我们有三种信息：

变量、人员和不同的时间段。保持一维常数，并使用第二维作为重复，可以在第三维的各个元素上获得叉积、协方差或相关矩阵。例如，我们可能会得到一个变量—逐变量相关矩阵，或人—逐人相关矩阵或逐时间相关矩阵。

Cattell (1952) 对六种类型给出了不同的标签，其中在某个时间点相关矩阵逐个变量分解的因子分析称为 K 型因子分析，而一个人与一个人在某个时间点的相关矩阵的因子分析称为 K 型因子分析。时间称为Q型因子分析。

The second option is the choice of weights for making linear combinations.

This option is two—fold; judgmental methods and analytical methods. As the name implies, judgmental procedures only approximate some exact solutions and there is no statistical rationale for their choice. The best known of these procedures are centroid method, factor method and multiple group method. Among the analytical procedures which use the basic structure theorems of matrix algebra, the most widely known is the principal components analysis. Finally, both the judgmental awl analytical procedures give further options (particularly in a correlation matrix input) s to the diagonal values.

The third option is regarding the derivation of new (rotated) factors by linear transformation procedures. Once again, there are two broad types: judgmental or analytical. The judgmental procedures all date back to Thurstone’s simple structure principle whereby a factor is rotated to an extent that any one variable is highly loaded on one and only one factor.

The analytical procedures use a number of variations of this simple structure principle. The two most common analytical procedures are quartimax and varimax rotations. The third option is resorted to by researchers for better interpretation of the results, and has no statistical significance per so. It is also the most controversial aspect of factor analysis.

It is obvious that possible combinations of the three types of options and further sub options in each type generate hundreds of separate factor analyses.

译文：第二种选择是选择用于进行线性组合的权重。  英国作业代写 

这个选项是双重的；判断方法和分析方法。顾名思义，判断程序只是近似一些精确的解决方案，他们的选择没有统计依据。这些程序中最著名的是质心法、因子法和多组法。在使用矩阵代数基本结构定理的分析程序中，最广为人知的是主成分分析。最后，两个判断锥分析程序都给出了对角线值的进一步选项（特别是在相关矩阵输入中）。

第三个选项是关于通过线性变换程序推导新的（旋转的）因子。再一次，有两种广泛的类型：判断型或分析型。判断程序都可以追溯到瑟斯通的简单结构原理，即一个因素被旋转到任何一个变量在一个且只有一个因素上高度加载的程度。

分析程序使用了这种简单结构原理的多种变体。两种最常见的分析程序是最大四次方旋转和最大方差旋转。第三个选项是研究人员为了更好地解释结果而采用的，并且本身没有统计意义。这也是因子分析中最具争议的方面。

很明显，这三种选项的可能组合以及每种类型中的进一步子选项会生成数百个单独的因子分析。

Profile and Cluster Analysis

A second major multivariate technique is profile or cluster analysis. Profile analysis is a generic term for all methods concerning grouping of individuals. Cluster analysis is a generic term for all methods concerning grouping of variables. The procedures for both cluster and profile analysis are very similar, and hence we will refer to both of them as profile analysis.

Profile analysis involves at least two separate steps. The first is the, measurement of similarity between two persons or variables. The second is classification of persons or variables based on the similarity measures.

A series of cut—and-try methods have been proposed to perform profile analysis (Attneave, F. (1950), Cronbach, (1955)) Most of these calculate distance between two persons by putting them in some sort of space. In general, a person with his scores cm n variables is considered a point in n-dimensional space.

译文：轮廓和聚类分析

第二种主要的多变量技术是轮廓或聚类分析。 轮廓分析是所有涉及个体分组的方法的通用术语。 聚类分析是所有涉及变量分组的方法的总称。 聚类分析和轮廓分析的过程非常相似，因此我们将它们都称为轮廓分析。

剖面分析至少涉及两个独立的步骤。 第一个是测量两个人或变量之间的相似性。 第二个是基于相似性度量的人或变量分类。

已经提出了一系列切入即试的方法来执行轮廓分析（Attneave, F. (1950), Cronbach, (1955)），其中大多数方法通过将两个人放在某种空间中来计算两个人之间的距离。 一般来说，一个人的分数为 cm n 变量被认为是 n 维空间中的一个点。

The distance between two points gives a measure of similarity:

the greater the distance the less similar the two points. Then several arbitrary methods are available which specify the cut-off point for the marginal person to be included in a group.

The two most common distance measures are calculation of absolute differences and distances based on Pythagorean Theorem. Mathematically, they can be stated as:

译文：两点之间的距离给出了相似性的度量：  英国作业代写 

距离越大，两点越不相似。 然后可以使用几种任意方法来指定要包含在一个组中的边缘人的分界点。

两种最常见的距离度量是基于勾股定理计算绝对差和距离。 在数学上，它们可以表示为：

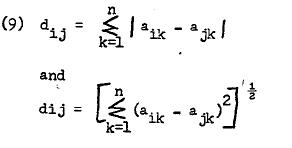
-where i and j are two persons or points in n-dimensional space constructed from measurement on k scales.
The similarity measured. in the above methods contains all the three types of information: level, dispersion and shape. By removing one or more of these, several other distance measures are possible.

Most of the profile analyses suffer from two problems.

First is the lack of invariance of similarity between two persons resulting from adding or dropping the dimensions on which they are measured. This becomes a serious issue when the dimensions for comparison are based on convenience and, at best, judgment instead of any theory. The second and related problem is the dimensions. If the dimensions are not orthogonal, the distances based on space become less meaningful.

译文：- 其中 i 和 j 是 n 维空间中的两个人或两个点，由 k 尺度上的测量构成。  英国作业代写

测量的相似度。 上述方法中包含了所有三种类型的信息：水平、分散和形状。 通过去除这些中的一个或多个，其他几种距离测量是可能的。

大多数剖面分析都存在两个问题。

首先是由于增加或减少测量他们的维度而导致的两个人之间缺乏相似性的不变性。 当用于比较的维度基于便利性，充其量是基于判断而不是任何理论时，这将成为一个严重的问题。 第二个相关的问题是尺寸。 如果维度不是正交的，则基于空间的距离变得没有意义。

Applications in Marketing  英国作业代写

The first attempts relate to measurement of similarity between self—concept and some consumer behavior variable where attempt is made to show greater congruence between the two (Birdwell, A. E. 1964). However, classification of consumers in these studies is already known based on the particular consumer behavior under investigation.

The pioneering efforts to measure similarity and then classify objects or people from Green, Frank and Robinson (1967). They used the distances to obtain clusters of cities which are potential for test marketing.

译文：在市场营销中的应用  英国作业代写 

第一次尝试涉及测量自我概念和一些消费者行为变量之间的相似性，其中试图显示两者之间的更大一致性（Birdwell, A. E. 1964）。 然而，这些研究中的消费者分类已经基于所调查的特定消费者行为而为人所知。

Green, Frank 和 Robinson (1967) 开创性地测量相似性，然后对对象或人进行分类。 他们使用距离来获得具有试销潜力的城市群。

Discriminatory Analysis

Discriminant analysis is useful in situations where total sample is divided into known groups based on some classificatory variable (sex), and the researcher is interested in understanding group differences or in predicting correct belonging to a group of a new sample based on the information on a set of predictor variables.

Discriminant analysis, therefore, can be considered either a type of profile analysis or a type of multiple regressions. As a profile analysis, its significance lies in the structure of weights obtained which discriminate various groups.

Then, it is sometimes referred to as structural analysis (King, 1967). As a multiple regression, its significance lies in providing predictive power to the researcher in terms of classifying individuals more accurately than by chance. In either case, the criterion variable is Single and classificatory.
Discriminant analysis entails transformation of scores of individuals on a set of predictor variables by using a set of linear weights.

The transformed value is called the discriminant score. This score is treated as projection of a point, on the discriminant axes and depending on whether it lies above or below the discriminant line, the individual is classified as belonging to one or the other group. The linear transformation of raw scores into discriminant scores can be represented as:

译文：判别分析  英国作业代写 

判别分析在以下情况下很有用：根据某些分类变量（性别）将总样本划分为已知组，并且研究人员有兴趣了解组差异或根据有关的信息预测新样本的正确归属一组预测变量。

因此，判别分析可以被认为是一种轮廓分析或一种多元回归。作为剖面分析，其重要性在于所获得的区分不同群体的权重结构。

然后，它有时被称为结构分析（King，1967）。作为多元回归，它的意义在于为研究人员提供比偶然更准确地对个体进行分类的预测能力。在任何一种情况下，标准变量都是单一和分类的。
判别分析需要通过使用一组线性权重来转换一组预测变量上的个人分数。

转换后的值称为判别分数。该分数被视为一个点在判别轴上的投影，并且根据它是位于判别线之上还是之下，个人被归类为属于一个组还是另一组。原始分数到判别分数的线性变换可以表示为：

This is analogous to one—may classification in analysis of variance.

It is possible to obtain more than one discriminant axis similar to factor analysis. However, the total number of axes does not exceed the number of groups minus one. In a two—group situation, therefore, only one discriminant axis and one discrirninant score for each individual are obtained.
Once the discriminant axis is obtained, the function could be tested for significance.

Then based on the discriminant scores, individuals in the sample void are classified in one of the groups. The proportion of correct classification then is compared against what could have been predicted by chance without any knowledge of the scores on the predictor variables. To this extent, it resembles the Bayesian approach.

译文：这类似于方差分析中的分类。 英国作业代写 

类似于因子分析，可以获得不止一个判别轴。 但是，轴的总数不超过组数减一。 因此，在两组情况下，每个个体只能获得一个判别轴和一个判别分数。
一旦获得判别轴，就可以测试该函数的显着性。

然后根据判别分数，样本空间中的个体被归入一组。 然后将正确分类的比例与在不了解预测变量分数的情况下偶然预测的比例进行比较。 在这方面，它类似于贝叶斯方法。

It is, however, more appropriate to validate the analysis by using the discriminant weights on another sample of individuals because predicting on the same sample from which coefficients are derived is shown to result in biases (Frank et al, 1965).