网络流和组合优化代写 ISE 632 – Problem set #1

ISE 632 – Problem set #1

网络流和组合优化代写 Let R and B be sets of n distinct red and blue points in the plane that are all in general position. Which is to say, no three

1. Let G be any network and let¯G denote its “opposite” network with the same set of vertices: that is, an edge (i, j) exists in G if and only if edge (i, j) does not exist in¯G , and vice versa. Prove that at least one of G and¯G is connected (by “connected” we mean that, for any two vertices i and j, there exists a path from i to j).  网络流和组合优化代写

2. Let R and B be sets of n distinct red and blue points in the plane that are all in general position. Which is to say, no three points are collinear. Prove that there always exists a perfect matching consisting of line segments between the members of R and the members of B such that no edges cross each other. (If you get stuck, this was a Putnam exam problem in the late 1970s readily available on the internet)

3. Recall that a network is regular if all of its vertices have the same degree, that is, the same number of edges incident to them. Suppose that G is a regular bipartite network where all nodes have degree d ≥ 1. Show that the edges of G can be decomposed into d disjoint perfect matchings.

4. 
   

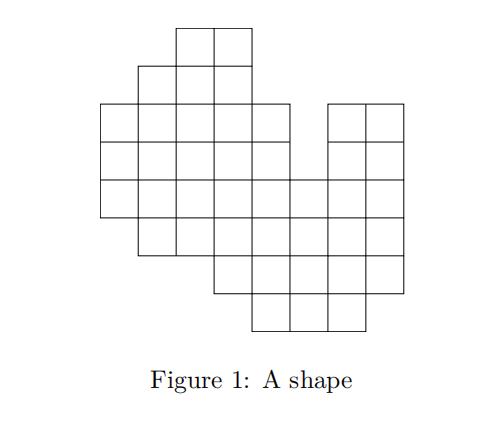
   Can the shape shown in Figure 1 be tiled with 2 ×1 rectangles?Give a tiling or show why none can exist.  网络流和组合优化代写

   
   

5. Suppose you have a network G = (V, E), not necessarily bipartite. Con sider the following “random” algorithm for obtaining a matching:

• Let M = ∅.


• 
  

  While there exists an edge e such that M ∪ e is a matching:– Add e to M.

  
  

• Return M.

In other words, “keep adding edges arbitrarily until you can’t add any more”. Prove that when this algorithm terminates.  The size of M is at least half the size of the maximum matching.  网络流和组合优化代写

更多代写：cs代写   经济代考   会计代写      计算机科学代写 内布拉斯加大学奥马哈分校代写