线性代数作业代写 LSE ST 2021/MA100R IRDAP

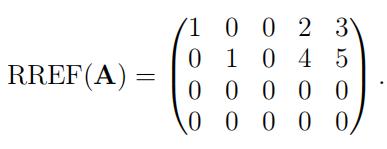
LSE ST 2021/MA100R IRDAP

线性代数作业代写 Find the numerical entries of the reduced row echelon form of the augmented matrix of the linear system Ax = −2c1 + c4 + c5

Question 1 线性代数作业代写

(a)     For x > 0, consider the homogeneous ordinary differential equation

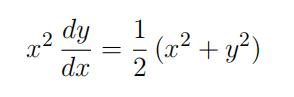
for the dependent variable y.

(i) Introduce a new dependent variable z by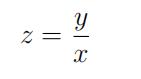and transform this homogeneous equation into a separable one for z.

(ii) Obtain the general solution of this separable equation in the form

G(x, z) = C

for some function G and arbitrary constant C.

(iii) Hence, obtain in the explicit form y = f(x) the unique solution of the homogeneous equation that satisfifies y = 5 when x = 1.

(b)

The hyperplane H ⇢ R4 tangent to the graph of a function g : R3 ! R at a point

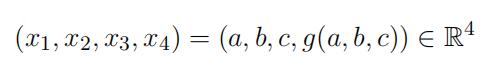
is described by the Cartesian equation  线性代数作业代写

2x1 − 5x3 + 3x4 = 8.

(i) Find the value of the directional derivative gu(a, b, c) in the direction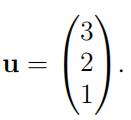

(ii) Find a unit vectorˆv  such that the directional derivative gˆv(a, b, c) in the directionˆv is equal

Question 2

(a)Find the unique solution of the system of differential equations  线性代数作业代写

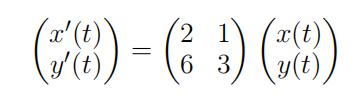
that satisfifies the conditions

x(0) = −1 and y(0) = 7.

(b)Find the unique solution of the ordinary differential equation

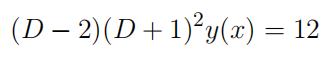
that satisfifies the conditions

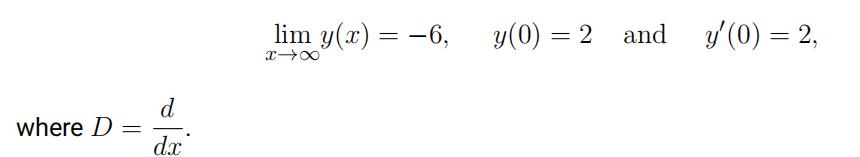
(c)Let c1, c2, c3, c4, c5 2 R4 denote the columns of a matrix A; that is,

A = (c1 c2 c3 c4 c5).

It is given that the reduced row echelon form of A is  线性代数作业代写

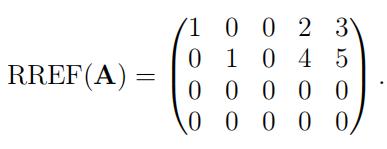
(i) Use the principle of linearity to fifind the general solution to the linear system

Ax = −2c1 + c4 + c5, expressing your answer in vector parametric form.

(ii) Find the numerical entries of the reduced row echelon form of the augmented matrix of the linear system Ax = −2c1 + c4 + c5, explaining your answer.

Question 3  线性代数作业代写

(a) Let E = {e1, e2, e3, e4} be the standard basis of R4 and let

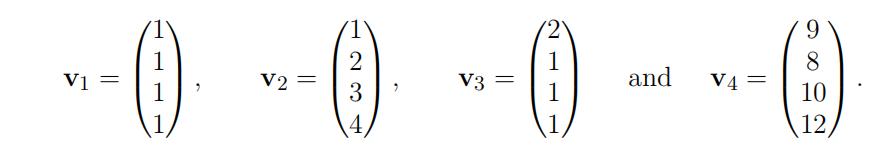
Consider a function F : R4 ! R4 that maps v1 to e1, v2 to e2, v3 to e3, and v4 to e4.

Explain why F cannot be a linear transformation.

(b)Let T : R5 ! R5 be a linear transformation given by  线性代数作业代写

T(x) = Mx,

where M is a symmetric matrix whose determinant is equal to− 36. The transformation T has the property that T(x) = 2x for all x in the subspace S1 ⇢ R5 given by

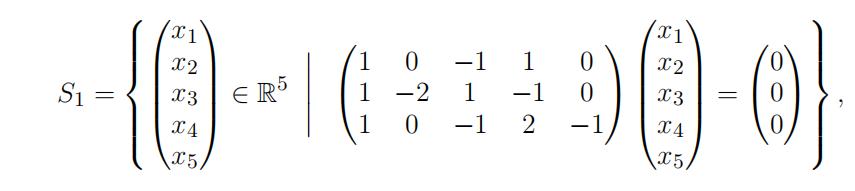
and T(x) = 3x for all x in the subspace S 2 ⇢ R5 given by

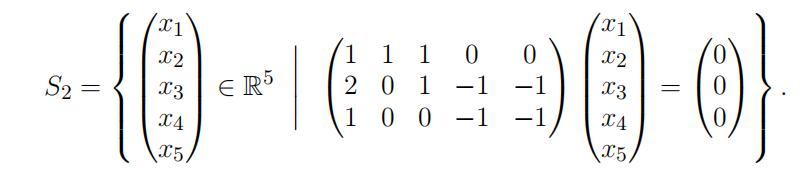
Find an invertible matrix P  and a diagonal matrix D  such that M  = PDP −1 , explaining your answer. You do not need to calculate M.

更多代写：cs代写   经济代考   会计代写      计算机科学代写 西顿霍尔大学代写