Exercises on Simple Linear Regression
线性代数代写 Drug designed to reduce smoking. A pharmaceutical company has developed a new drug designed to reduce a smoker’s reliance on tobacco.
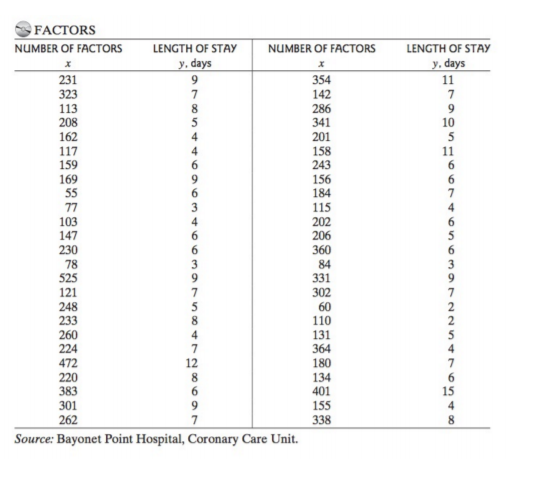
1. Caring for hospital patients. Any medical item used in the care of hospital patients is called a factor. For example, factors can be intravenous tubing, intravenous fluid, needles, shave kits, bedpans, diapers,
dressings, medications, and even code carts. The coronary care unit at Bayonet Point Hospital (St. Petersburg, Florida) investigated the relationship between the number of factors per patient, x, and the
patient’s length of stay (in days), y. The data for a random sample of 50 coronary care patients are given in the following table, while a SAS print-out of the simple linear regression analysis is shown on the next page. 线性代数代写

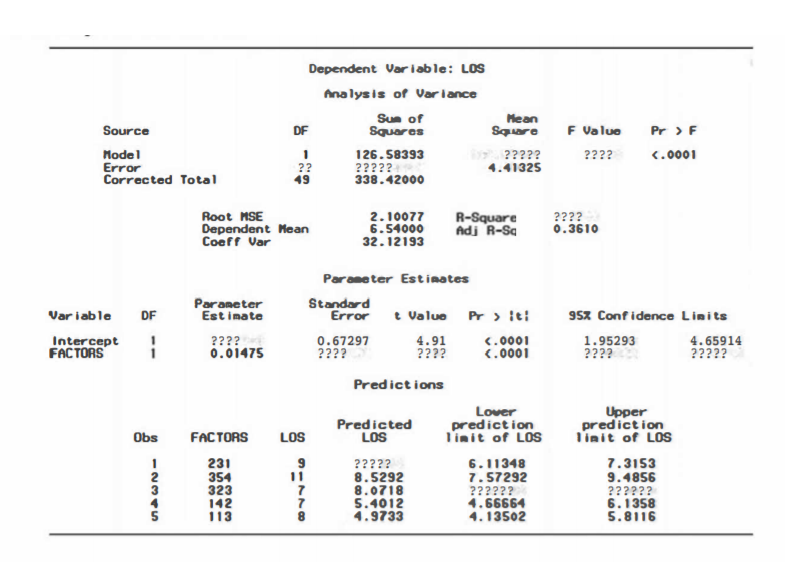
Using the SAS output, answer the following questions:
a. Fill out the missing components in the SAS output. You might need the following calculations:
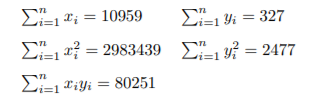
b. Write the formula for the least squares line for the data
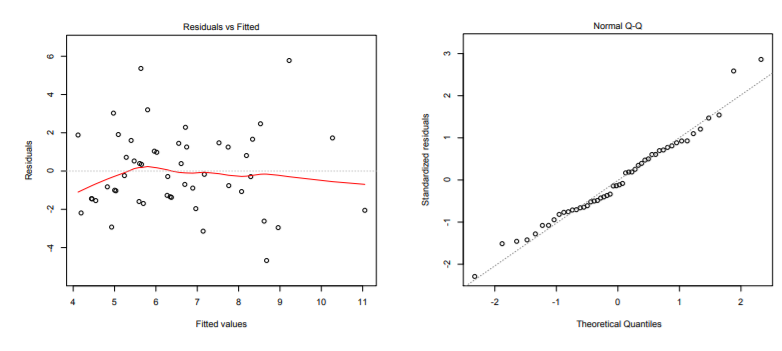
c. Using the SAS output and the plots given below check the assumptions of the regression fit. Are all of the assumptions satisfied? Explain the information you used (which plot, which result in the output) to check the assumptions. Do you need further information for any of the assumptions?
d. Define β1 in the context of this problem and interpret its estimate.
e. Test the hypothesis that the number of factors per patient (x) contributes no information for the prediction of the patient’s length of stay (y) when a linear model is used (use α = .05). Draw the appropriate conclusions.
f. Find a 95% confidence interval for β1. Interpret your results.
g. Find the coefficient of correlation for the data. Interpret your results.
h. Find the coefficient of determination for the linear model you wrote in part b. Interpret your result.
i. Find a 95%prediction interval for the length of stay of a coronary care patient who is administered a total of x = 231 factors. Interpret this interval.
2. English as a second language reading ability. What are the factors that allow a native Spanishspeaking person to understand and read English? A study published in the Bilingual Research Journal (Summer 2006) investigated the relationship of Spanish (first language) grammatical knowledge to English (second language) reading. The study involved a sample of n = 55 native Spanish-speaking adults who
were students in an English as a second language (ESL) college class. Each student took four standardized exams: Spanish grammar (SG), Spanish reading (SR), English grammar (EG), and English reading
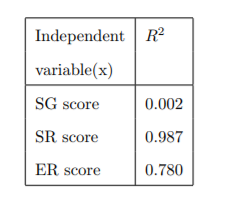
(ESLR). Simple linear regressions were used to model the ESLR score (y) as a function of each of the other exam scores (x). The results are summarized in the table. 线性代数代写
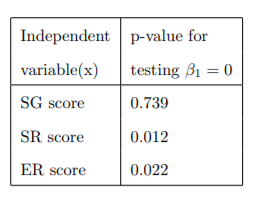
a. At α = 0.05, which variable(s) is linearly related to ESLR score? Explain.
b. The coefficient of determination values are listed below, based on these values, which variable should be used to fit a linear regression to predict ESLR score? Explain.
3. Drug designed to reduce smoking. A pharmaceutical company has developed a new drug designed to reduce a smoker’s reliance on tobacco. Since certain dosages of the drug may reduce one’s pulse rate to dangerously low levels, the product-testing division of the pharmaceutical company wants to model the relationship between decrease in pulse rate, y (beats/minute), and dosage, x (cubic centimeters). Different dosages of the drug were administered to eight randomly selected patients, and 30 minutes later the decrease in each patient’s pulse rate was recorded. The results are given in the accompanying table.
Initially, the company considered the model y = β1x + ε since, in theory, a patient who receives a dosage of x = 0 should show no decrease in pulse rate (y = 0).
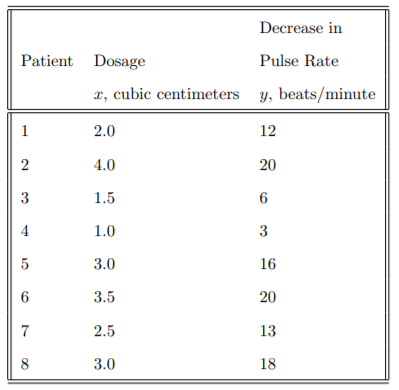
a. Fit a straight-line model that passes through the origin.
b. Is there evidence of a linear relationship between drug dosage and decrease in pulse rate? Test at α = 0.10.
c. Find a 99% prediction interval for the decrease in pulse rate corresponding to a dosage of 3.5 cubic centimeters.
d. Did we make the right decision in fitting a model without the intercept following the company’s advice or should we have included an intercept in our model?





发表回复
要发表评论,您必须先登录。