8 practice problems.
算法作业代写 For the dynamic array problem (see class notes), consider handling insertions and deletions. Assume that deletion always involves
1. There are n ≥ 2 people standing in line. They all have different heights. Each person independently takes a step forward if there is nobody standing next to them that is taller. For example, if the heights are:
183, 187, 198, 175, 181 (cm), then the third and fifth person step forward. Show formally how many people we expect to step forward.
2. We release k bees in a field with n flowers. k might be smaller, equal, or larger than n. Each bee goes to some random flower. Multiple bees can land on the same flower. 算法作业代写
(a) What is the expected number of bees that will visit each flower?
(b) How many flowers do we expect will be visited?
(c) Does your solution for (b) confirm the intuitive answer for the special case where there is only one flower? Or what if there’s only one bee?
3. CLRS Problem 8-4. Summary: you have n red jugs and n blue jugs. All the red jugs have distinct capacities, and each one matches the volume of one blue jug. They all have weird shapes so you can’t tell which holds more. The only way to distinguish (compare) is to fill a jug with water and then pour the water into another jug (there are 3 possible outcomes). You are not allowed to pour water from a red jug to another red jug, or from a blue jug to another blue jug.
(a) Show how to match all the red jugs to blue jugs, in O(n2) time.
(b) Show that obtaining this matching requires Ω(n log n) comparisons in the worst-case (for any strategy).
(c) Show that the matching can be obtained in O(n log n) expected time. ps - you have as much water as you like.
4. In a fully balanced (aka complete, symmetric) binary search tree (BST) with n nodes, the root has rank d n2 e. Given a red-black tree, how extreme (e.g., how low) could the rank of the root be? Use Θ-notation for your answer, otherwise lower order terms may become annoying. Include a description or drawing of a tree that corresponds to your answer (in other words explain how you’re getting your answer).
5. Let S be a set of n rectangles (aka boxes) of various sizes in 2D, each of which has only horizontal and vertical edges. You may assume that no two edges are on the same line. Two boxes overlap if their interiors have at least one point in common. 算法作业代写
(a) Give an O(n log n)-time algorithm that decides if there is a pair of boxes in S that overlap, and produces one such pair if it exists.
Hint: Think about a horizontal line that moves vertically, starting from above S and ending up below. See the red line in the figure below.
(b) Extend your algorithm slightly, to also report all the pairs of boxes in S that overlap, assuming that there are only O(n) overlapping pairs overall.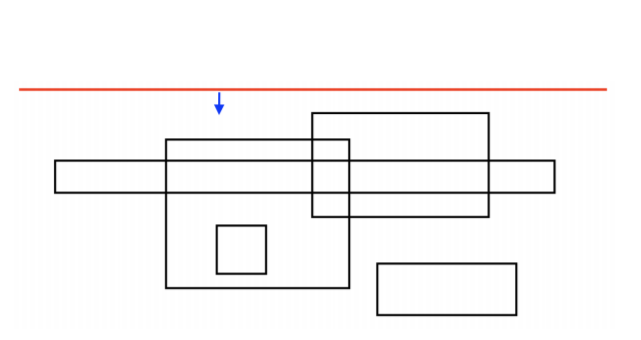
6. Consider a set S of 2n line segments in 2D: n horizontal and n vertical. Assume that no segment has endpoints at the same x-coordinate or y-coordinates as any other segment. Provide a sub-quadratic-time algorithm (i.e., Θ(n2) doesn’t suffice) to count how manyintersections there are among the segments in S. Note that you do not need to list the intersections. Just report how many there are. In the example below the output is: 5.
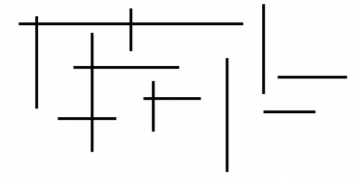
- For the dynamic array problem (see class notes), consider handling insertions and deletions. Assume that deletion always involves the rightmost element in the array. At any moment, the array storing your data must have a size that is Θ(k), where k is the number of elements currently stored. In other words, you don’t want to be occupying too much empty space. This means that at some point you might have to downsize, i.e., copy all the data into a smaller array.
(a) When should you double and when should you downsize, to get low amortized cost?
(b) Explain (informally, if you wish) why the amortized cost is low for your strategy.
8. You must support the following two operations on a set of numbers: (1) insertion, and (2) “large-delete” which is to delete the largest half of the values in the set. In other words if there are k elements you delete the elements with the dk/2e largest values. Both operations should take constant time, amortized. Assume that you start with an empty data structure. 算法作业代写
(a) What data structure will you use, and how will you handle the operations? What is the worst-case time complexity for one operation?
(b) Show why each operation costs O(1) amortized. You should try both accounting and the potential method.





发表回复
要发表评论,您必须先登录。