最优化理论作业代写 comprehensive assignment for second

APM462 HW10
comprehensive assignment for second term1

最优化理论作业代写 In lectures we derived the Lagrange multiplier condition for a constrained minimization problem with one constraint using the

This is your final assignment for APM462. I hope you found the  course interesting, challenging, and enjoyable. Good luck. Jonathan.
(1) In lectures we derived the Lagrange multiplier condition for a constrained minimization problem with one constraint using the 1st order condition for unconstrained minimization in the special case when the surface is the graph of a function. That is we derived the Lagrange multiplier condition for the problem

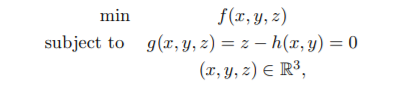
by converting the problem into the unconstrained problem

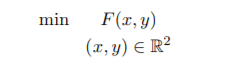
where F(x, y) := f(x, y, h(x, y)) and then using the condition ∇F(x∗, y∗) =0 to conclude

∇f(x∗, y∗, z∗) + λ∇g(x∗, y∗, z∗) = 0.

Here you are asked do the same thing for two constraints. That is, starting with the problem  最优化理论作业代写

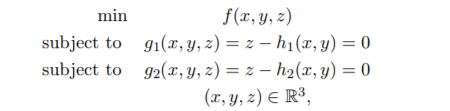
derive the Lagrange multiplier condition ∇f + λ1∇g1 + λ2∇g2 = 0 by first converting the problem to an unconstrained minimization problem as follows. Let (x∗, y∗
, z∗) be a local minimum of f subject to the two constraints and assume (x∗, y∗, z∗) is a regular point, so ∇g1(x∗, y∗, z∗) and ∇g1(x∗, y∗, z∗) are linearly independent. Assume further the we are in the special case where the intersection of the two surfaces g1 = 0 and g2 = 0 is a curve C which is parametrized by a function of x. That is C = {(x, φ(x), ψ(x)) | x ∈ R} for some C1 functions φ, ψ : R → R. Now convert the original constrained problem into the following unconstrained problem:

min F(x)
x ∈ R

where F(x) := f(x, φ(x), ψ(x)) and use the condition ∇F(x∗) = 0 to conclude

∇f(x∗, y∗, z∗) + λ1∇g1(x∗, y∗, z∗) + λ2∇g2(x∗, y∗, z∗) = 0.

(2) Consider the optimization problem: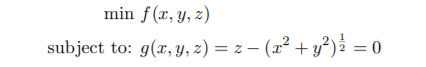

Note that {g = 0} is a cone with vertex at the origin. Also note that g is not diffferentiable at the origin.

(a) Find all the regular points of the surface {g = 0} \ {(0, 0, 0)}.

(b) Suppose f(x, y, z) = z. Use the 1st order neccessary conditions for a local min to find the candidates for minimizers and then solve the optimization problem.

(c) Suppose f(x, y, z) = ax + cz where a, c ∈ R. Use the 1st order neccessary conditions for a local min to find the candidates for minimizers and then solve the optimization problem. Hint: you should consider different cases depending on the values of a, c.

(3) Prove that the convex hull of finitely many points is a compact set. That is, for x1, . . . , xk ∈ Rn, show that S := {λ1x1 + · · · + λkxk | λi ≥ 0, λ1 + · · · + λk = 1} is compact.

(4) Consider the optimization problem:  最优化理论作业代写

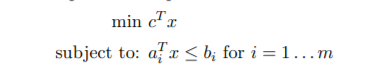
here x ∈ Rn, 1 ≤ m < n, and the ai’s are linearly independent. Assuming a minimizer exist, let x∗ and µ∗satisfy the 1st order necessary Kuhn-Tucker condition.
(a) Prove that µ∗is unique.
(b) Suppose c = −aj some j and that the all the active constraintsat x∗ are strongly active. Prove that x∗is not unique.
(5) Let u∗(t) = (x∗(t), y∗(t)) satisfy the Euler-Lagrange equation to the following problem: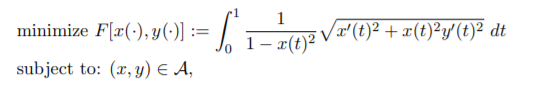

更多代写： HomeWork cs作业     金融代考    postgreSQL代写         IT assignment代写     统计代写  巴尔德摩县社区学院代写