数学群论作业代写 MAT301 Week 5 Exercises

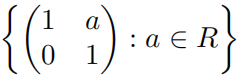
MAT301 Week 5 Exercises

数学群论作业代写 Describe all homomorphisms from the additive group Q to itself. Conclude that there is no injective homomorphism from Q to itself

Exercise 1. Prove that the group of integers is isomorphic to all of its non-trivial subgroups.

Exercise 2. Let G be a group and let φ be an automorphism of G. Prove that the set of elements of G that are fifixed by φ is a subgroup of G.

Exercise 3. For R = Z, R, Q, C, what group is the multiplicative group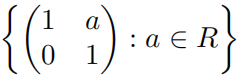isomorphic to? 数学群论作业代写

Exercise 4. Let G be an abelian group and let φ : G → G be the homomorphism defifined by φ

1. Suppose that G is fifinite. Describe when φ is an automorphism of G.


2. Given an example of an infifinite group G such that φ is injective, but not surjective.

Exercise 5. Let G be a group. For each g ∈ G, let Inn(g) be the inner automorphism of G determined by g, that is, Inn(g) : G → G is defifined b

1. Let g ∈ G. When is Inn(g) = idG? When is Inn(G) = {idG}?


2. Let g1, g2 ∈ G. When is Inn(g1) = Inn(g2)?


3. Prove that the map Inn : G → Inn(G) is a homomorphism. What is its kernel?

Exercise 6. Let G and H be isomorphic groups and let φ, ψ : G → H be isomorphisms. Prove that {x ∈ G : φ(x) = ψ(x)} is a subgroup of G.   数学群论作业代写

Exercise 7. Prove that the dicyclic group Dic5 of order 20 is not isomorphic to the dihedral group D10 of order 20.

Exercise 8. Prove that R × is not isomorphic to the multiplicative group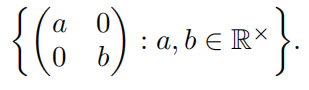

Exercise 9. Find an injective homomorphism φ : Q>0 → Q>0 that is not surjective. Conclude that Q>0 is isomorphic to a proper subgroup of itself.

Exercise 10. Describe all homomorphisms from the additive group Q to itself. Conclude that there is no injective homomorphism from Q to itself that is not surjective, and therefore Q is not isomorphic to a proper subgroup of itself.

Exercise 11. Prove that Q× is not isomorphic to Q.  数学群论作业代写

Exercise 12. Let φ ∈ Aut(R ×). Prove that φ(R>0) = R>0 and φ(R<0) = R<0.  数学群论作业代写

Exercise 13. Let φ : G → H and ψ : H → K be homomorphisms. How are ker φ and ker(ψ ◦ φ) related?

Exercise 14. Let φ : G → H be a surjective homomorphism. Prove that φ(Z(G)) ⊆ Z(H). Can you fifind a counterexample for this result if you drop the assumption that φ is surjective?

Exercise 15. Let G be a fifinite group. Prove that G is abelian if and only if there exists an automorphism φ of G such that

1. φ 2 = id; and


2. for all x ∈ G, we have φ(x) = x if and only if x = e.

(Hint: The “only if” direction is easier and holds even in the case when G is not fifinite. For the “if” direction, prove that if an automorphism φ of G with the above properties exists, then for all x ∈ G there exists y ∈ G  such that x = φ(y)y −1 , and think about what this tells you about φ(x). How can you prove that for all x ∈ G there exists y ∈ G such that x = φ(y)y −1 without explicitly determining y? Make sure you use the hypothesis that G is fifinite!)

更多代写：计算机作业代写    经济代考   essay代写      AI作业代写  华盛顿州立大学申请代写