MAT334 Complex Variables
数学复数作业代写 I have read and understand the rules for collaboration on problem sets described in the Homework Policies. I have not violated these
Instructions 数学复数作业代写
This homework is based on week 3. Please read the Homework Policies for details on submission policies, collaboration rules, and general instructions.
• Office hours are held throughout the week. During office hours, you may discuss the problems with peers and the Instructor/TA. However, you may not outright share your solutions with your peers.
• Submit your polished solutions on Crowdmark. Do not submit rough work. Organize your work neatly. You may be penalized for work that is disorganized, messy, or illegible. Do not send anything by email. Late submissions are not accepted under any circumstance. Remember you can resubmit anytime before the deadline.
• Show your work and justify your steps on every question, unless otherwise indicated. Partial credit will not be given for answers without justification, unless otherwise indicated.
• Each submission must include a signed copy of the Academic Integrity statement. You can find this statement below. Each member of your group must write out and sign their statement. This will be the first question on Crowdmark. Failure to attach Academic Integrity statements from each group member will result in a grade of zero for the group. 数学复数作业代写
Academic integrity statement
I confirm that:
• I have read and followed the policies described in the Homework Policies.
• I have read and understand the rules for collaboration on problem sets described in the Homework Policies. I have not violated these rules while writing this problem set.
• I understand the consequences of violating the University’s academic integrity policies as outlined in the Code of Behaviour on Academic Matters. I have not violated them while writing this assessment. By signing this document, I agree that the statements above are true.
Date:
Signature: 数学复数作业代写
- In this question, you will disect a bad argument using branches. Consider the claim below:
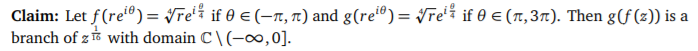
The argument below is incomplete and possibly incorrect. 数学复数作业代写
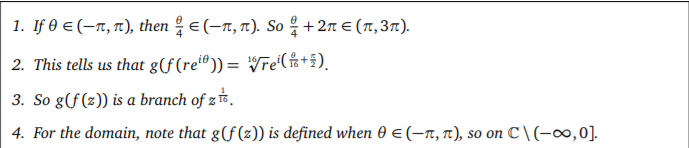
(1a) (1 point) Line 2 is trying to show something about the number g(f (z)) for some fixed z. Precisely state what it is trying to show. (Note: it is not showing anything about the function g(f (z)).)
(1b) (1 point) Line 3 claims that line 2 shows g(f (z)) is a branch. However, it is not fully justified. What else do you need to show to conclude it is a branch?
(1c) (1 point) Finish properly justifying line 3.
(1d) (1 point) Line 4 does not consider every situation where g(f (z)) is not defined. What other case needs to be handled?
(1e) (1 point) Find the actual domain of g(f (z)) by finishing the argument.
2. Let arg0 数学复数作业代写
(z) be the branch of the argument with arg0 (z) ∈
In this question, you will prove that g(z) = f (f (z)) is a branch o
(2a) (4 points) The claim that g(z) is a branch o
is really two smaller claims. Precisely state these smaller claims and explain why these claims show g is a branch o
(2b) (1 point) Prove that g is a brach o
发表回复
要发表评论，您必须先登录。