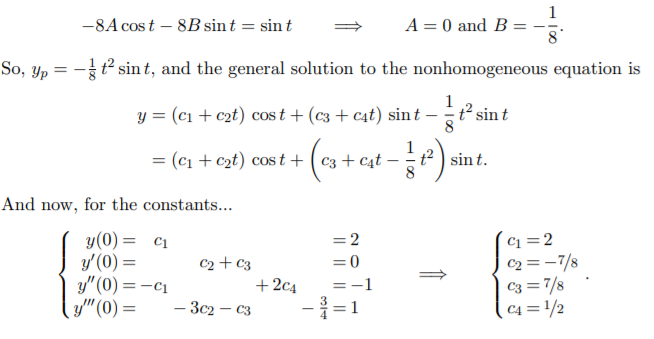
Math 3F — Exam #2 Sample
数学代写Exam代写 For each equation below, write the form of the guess you would use in using the method of undetermined coefficients.
1. Solve each equation or initial-value problem 数学代写Exam代写
(a) y′′ + 8y′ − 9y = 0, y(1) = 1, y′(1) = 0
(b) 4y′′ + 12y′ + 9y = 0, y(0) = 1, y′(0) = −4(c) y′′ + 6y′ + 13y = 0
- For each equation below, write the form of the guess you would use in using the method of undetermined coefficients. Do not determine the coefficients. Note that the equations are very similar to the ones in the preceding problem.
(a) y′′ + 8y′ − 9y = t cost
(b) 4y′′ + 12y′ + 9y = 2te− 32t
(c) y′′ + 6y′ + 13y = et sin 2t - Solve one of the equations in the preceding problem using variation of parameters.
4. Solve the IVP:
y(4) + 2y′′ + y = sin t; y(0) = 2, y′(0) = 0, y′′(0) = −1, y′′′(0) = 1.
5. Solve each equation or initial-value problem.
(a) y′′ + 8y′ − 9y = 0, y(1) = 1, y′(1) = 0
(b) 4y′′ + 12y′ + 9y = 0, y(0) = 1, y′(0) = −4
Solutions to Exam #2 Sample
Laney College, Spring 2021
Fred Bourgoin
1. Solve each equation or initial-value problem.
(a) y′′ + 8y′ − 9y = 0, y(1) = 1, y′(1) = 0
Solution. The characteristic equation is r2 + 8r − 9 = 0 which has rootsr = −9 and 1, so the general solution is y = c1e−9t + c2e t . The initial conditions yield
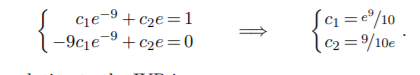
Hence, the solution to the IVP is
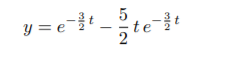
(c) y ′′ + 6y ′ + 13y = 0 Solution. The characteristic equation is r 2 + 6r + 13 = 0 and has complex conjugate roots r = −3 ± 2i, so the general solution is
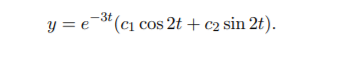
- For each equation below, write the form of the guess you would use in using the method of undetermined coefficients. Do not determine the coefficients. Note that the equations are very similar to the ones in the preceding problem.
(a) y′′ + 8y′ − 9y = t cost Solution. Guessing yp = (At + B) cost + (Ct + D) sin t does not interfere with the yc we found in Problem 2(a), so that’s the right guess.
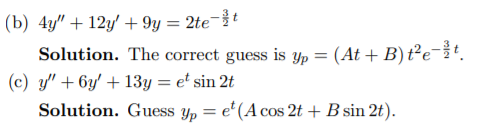
- Solve one of the equations in the preceding problem using variation of parameters. Solution. The easiest one to solve using variation of parameters is Problem 3(b). Since we had
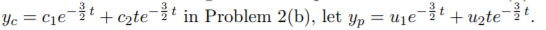 We then need to solve the system
We then need to solve the system
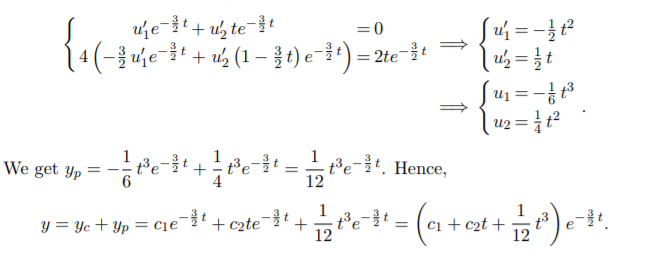
4. Solve the IVP: 数学代写Exam代写
![]()
Solution. Begin by solving the corresponding homogeneous equation, whose characteristic equation r 4 + 2r2 + 1 = 0 has repeated roots r = ±i. The general solution is
yc = (c1 + c2t) cost + (c3 + c4t) sin t.
For a particular solution, guess yp = At2 cost + Bt2 sin t. Differentiating it four times and plugging it into the equation, we end up with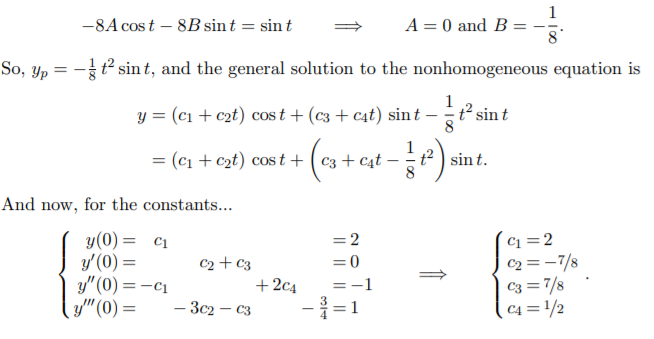






发表回复
要发表评论,您必须先登录。