Engineering Physics 2
Assessment Component 4: Rigid Body Dynamics &
Course Review
工程物理代写 Consider the rotor in Figure 6. The rotor consists of two point masses, while the rest of the structure has negligible mass.
This is an assessed worksheet for Engineering Physics 2 (EMAT20010). The total mark for the assessment for Engineering Physics 2 is 200. This component is worth 80 marks. You should attempt all questions. Once you have completed the worksheet, upload your solutions and working to the submission point on the Engineering Physics 2 Blackboard page. If you have written your solutions on paper you will need to scan them and upload the scan.
Your submission must be a single le in PDF or DOCX format.
Before uploading the scan of your work, please ensure that: 工程物理代写
your writing, and any necessary gures, are legible on the scan (note that this may require you to rewrite your solutions after your rst attempts.)
you have included all relevant working,
solutions to each question (and subquestion) are clearly labelled and some space is left between questions.
The deadline for submitting your work online is 22nd January 2021, 13:00GMT. If you need an extension to this deadline due to extenuating circumstances, you must arrange this with the SCEEM School
Oce.
You should not work with anyone else on this worksheet. All work must be your own. Plagiarism will be dealt with according to the University's Plagiarism Policy. Deadline: 22nd January 2021, 13:00GMT
Total Marks: 80
This final component of the assessment has questions that will test your knowledge of the whole unit. Question 1 relates to Section I of the notes. Questions 2 and 3 relate to Section II of the notes. Question 4 relates to Section III of the notes. Questions 5 and 6 relate to Section IV of the notes.
Question 1.
Consider the mechanism in Figure 1, which consists of two rigid bodies, an equilateral triangle (1) and a rod (2). The rod is of length l m long and all sides of the triangle are also l long. The two bodies are connected in a pin joint at point B. The triangle (1) rotates about point P (the origin of the coordinate system). The end of the rod, denoted by C slides along the ground horizontally. The direction of rotation is indicated in Figure 1. The acceleration of point C (denoted by |aC|m s−2 ) is constant. At the instant shown the distance between P and C is also l.
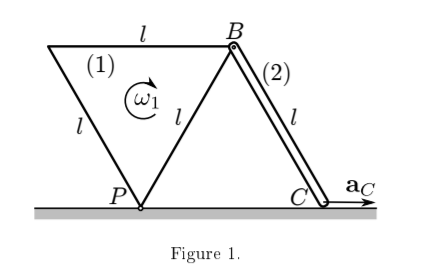
(a) (i) Determine the velocity of point B. 2 mark(s)
(ii) Draw a diagram to indicate the position of the zero-velocity point of rod (2). Calculate its position. 4 mark(s)
(iii) What is the velocity of point C (vC) and the angular velocity (ω2 ) of the rod (2)? 3 mark(s)
(b) (i) Find two expressions for the acceleration of point B (aB): one in terms of l, ω1 and ε1, and one in terms of l, ω1, ac and ε2. 3 mark(s)
(ii) Solve the equations arising in Q1(b)(i) for the angular accelerations of the two rigid bodies and for the acceleration of point B. 3 mark(s)
(c) What should be the acceleration of point C so that the triangle rotates with constant angular speed? 1 mark(s) 16 marks total
Question 2. 工程物理代写
(a) Consider the mechanism in Figure 2. Two equal point masses m are connected by a spring and a rope through a pulley mechanism. Each of the two point masses can only move vertically. The pulley has negligible mass and negligible radius. The vertical part of the rope (on the right side of the pulley) is inextensible. The spring connecting the two point masses has stiness k, natural length of zero and d denotes the extension of the spring. The pulley remains xed, so as the left mass moves vertically the spring moves freely to form an angle with the horizontal.
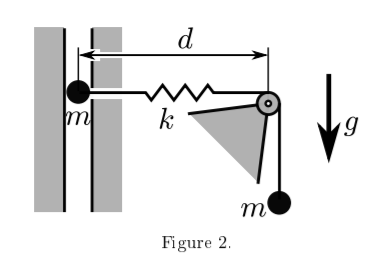
(i) How many degrees of freedom does the mechanism have? Determine a suitable number of generalised coordinates that describe the motion of the mechanism.Draw a diagram to illustrate this.2 mark(s)
(ii) Determine the kinetic and potential energies of the mechanism as functions of the generalised coordinates.2 mark(s)
(iii) Using the Lagrangian formalism, derive the equations of motion of the point masses. 3 mark(s)
(b) Assume that a mechanical system (unrelated to part (a)) has two generalised coordinates x and y. The kinetic and potential energies are
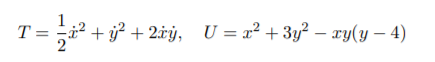
(i) Find all equilibria of the system.4 mark(s)
(ii) Determine the mass and stiness matrices of the system at the equilibrium x = 0, y = 0.3 mark(s)
(iii) What are the natural frequencies and the corresponding mode shapes about the equilibrium x = 0, y = 0? 3 mark(s)17 marks total
Question 3.
Consider the two degrees of freedom mechanism illustrated in Figure 3. The uniform disc of radius R can rotate around its centre of mass A in the x − y plane. At point B on the rim of the disc a uniform rod of length l is connected through a pin joint to the disc. The straight line between A and B makes an angle ϕ with the vertical direction down from A as shown (with ϕ measured in an anticlockwise direction from this vertical direction). The centre of mass of the rod is at point C. The angle between the rod and the vertical direction down from B is given by ψ as shown (with ψ also measured in an anticlockwise direction from this vertical direction). The mass of the disc and the rod are m1 and m2 respectively.
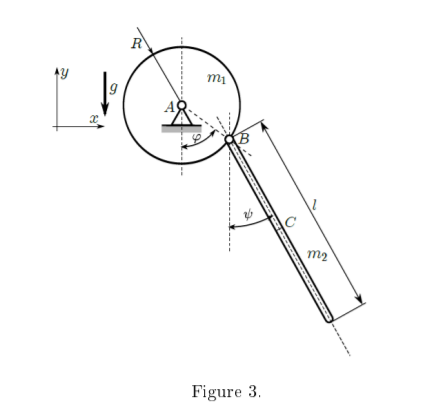
(a) Use ϕ and ψ as generalised coordinates. Calculate the velocity of the point B in terms of R and ϕ and hence determine the velocity of point C. 3 mark(s)
(b) Use part (a) to calculate the kinetic and potential energies of the system. 4 mark(s)
(c) Use a Lagrangian approach to derive the equations of motion for the system. 3 mark(s) 10 marks total
Question 4.
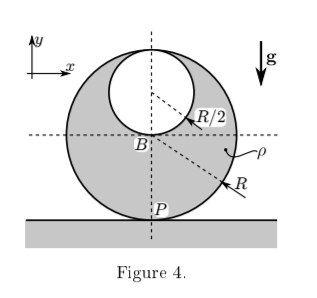
Consider a disc, illustrated in Figure 4, rolling without slipping on the ground. The material of the disc is homogeneous with area density ρ = 1/π kg/m2 . The radius of the disc is R and it has a circular hole cut out with radius R/2 as shown.

(a) (i) Find the centre of mass D of the disc with a hole, as illustrated in Figure 3, relative to point B. 3 mark(s)
(ii) Using the parallel axes theorem, calculate the moment of inertia of the disc withthe hole about point D. 3 mark(s)
(b) (i) Assume that the disc with the hole in the depicted position has zero potential energy. What is the potential energy of the disc when it rotates to the left by an angle ϕ? 2 mark(s)
(ii) Calculate the velocity of the centre of mass of the disc as a function of its rotation ϕ and its angular velocity ϕ˙. 4 mark(s)
(iii) Write down the equation of motion of the disc using Lagrange's equation and ϕ as the generalised coordinate. 2 mark(s)
(iv) Calculate the equilibria of the disc. Which equilibrium is stable? 2 mark(s) 16 marks total
Question 5.
A solid, homogenous cylinder (2) is mounted on top of a turntable (1) as shown in Figure 5. The radius of the cylinder is R and its length is h. The angular velocity of the turntable is constant and equals ω1 = krad s−1 . At the instant shown the instantaneous angular velocity of the cylinder is ω2 = 2i + krad s−1.
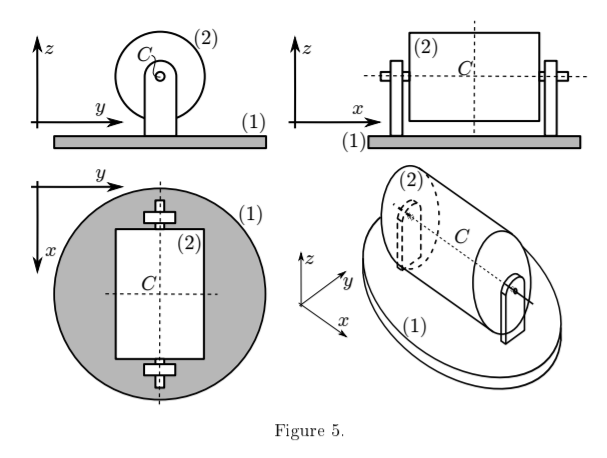
(a) What is the angular acceleration (ε2) of the cylinder (2)?1 mark(s)
(b) What is the moment of inertia tensor of the cylinder about point C in the depicted position? 1 mark(s)
(c) What torque MC must there be at point C as a result of the reaction forces to keep the cylinder in its current kinematic state? 2 mark(s) 4 marks total
Question 6. 工程物理代写
Consider the rotor in Figure 6. The rotor consists of two point masses, while the rest of the structure has negligible mass.
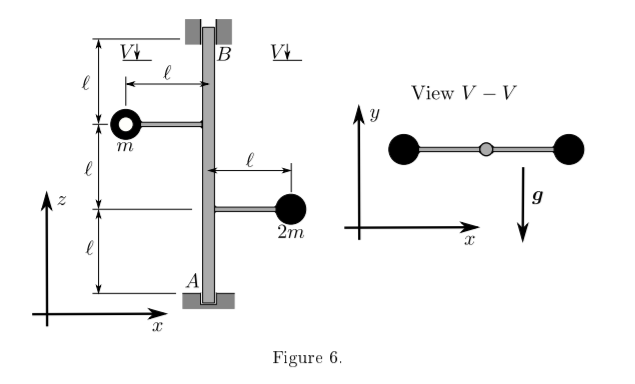
(a) (i) Taking A to be the origin, calculate the centre of mass of the rotor rAC. 2 mark(s)
(ii) Calculate the moment of inertia tensor of the rotor for point A. 2 mark(s)
(iii) Using the parallel axes theorem, calculate the moment of inertia tensor of the rotor for its centre of mass C. 2 mark(s)
(b) Assume that the rotor has an angular velocity ω = krad s−1.
(i) Draw free-body diagrams of the rotor that show the reaction forces at A and B, the force due to gravity on the two masses, the acceleration of the centre of mass (aC) and the angular acceleration (ε). 2 mark(s)
(ii) Calculate the acceleration of the centre of mass (aC) of the rotor in terms of ε and l. 2 mark(s)
(iii) Use Newton's second law to relate the reaction forces at A and B to aC.2 mark(s)
(iv) Calculate the moment at point A (MA) in terms of m, g, l and the reaction force at B. 2 mark(s)
(v) By equating the rate of change of angular momentum (H˙ A) at A to MA, express the reaction forces at A and B, and the angular acceleration (ε) in terms of m, g and l. 3 mark(s) 17 marks total





发表回复
要发表评论,您必须先登录。