发展经济学代写 ECON 4784: Economic Development

ECON 4784: Economic Development

发展经济学代写 Why stop at sharecropping? Risk-averse tenant will prefer a fixed wage (income) contract equal to EV of sharectopping return

Notes on The Market for Land (Chapter 12—Debraj Ray, Development Economics, 1998)

What kind of incentive scheme will maximize economic surplus (output net of costs)?

We have already discussed problems of incentivizing workers under fixed wage scheme, so we know fixed wage does not maximize economic surplus.

Here we will focus on comparing fixed rent (FR) and sharecropping (SC) contracts. Both contracts can be generalized as follows:

Let R = αY + F, where R is what landlord gets from farmer, Y is output, and F is a constant.

If α=0, F>0 : Fixed Rent (FR) contract with rent F

If F=0, 0<α<1 : Sharecropping (SC) contract with landlord’s share = α and tenant’s share =1-α.

If the effort of the tenant cannot be monitored, the tenant has an incentive to under-supply effort.  发展经济学代写

To give the tenant correct incentives, he must be the sole residual claimant of the output (i.e. α=0).

Intuition: If you are a farmer considering whether to work an additional hour, will you be more likely to work the extra hour if you get 100% of the output produced from that extra hour or if

you get some fraction of the output of that extra hour?

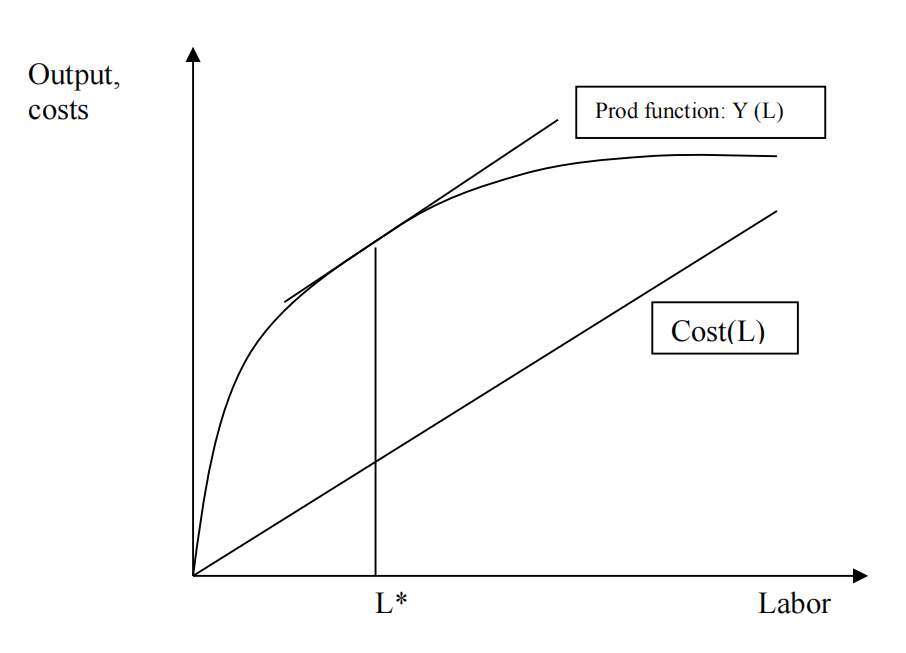
Plot a production function that relates output to labor:

Labor supply to the rented plot has a cost because this labor could be working on another plot (opportunity cost), or the farmer may simply value his leisure.

The economic surplus produced by the tenancy arrangement is the difference between output and costs (vertical difference). The surplus varies with the amount of labor supplied. We’re interested

in the labor input level that leads to the maximum surplus (L*). At this point, the tangent to the production function has a slope equal to the cost curve. Why? Because the marginal product of

labor is equal to the opportunity cost of labor.Output,costs LaborL*Prod function: Y (L) Cost(L)3

In a Sharecropping contract, the tenant’s labor returns looks like the following:

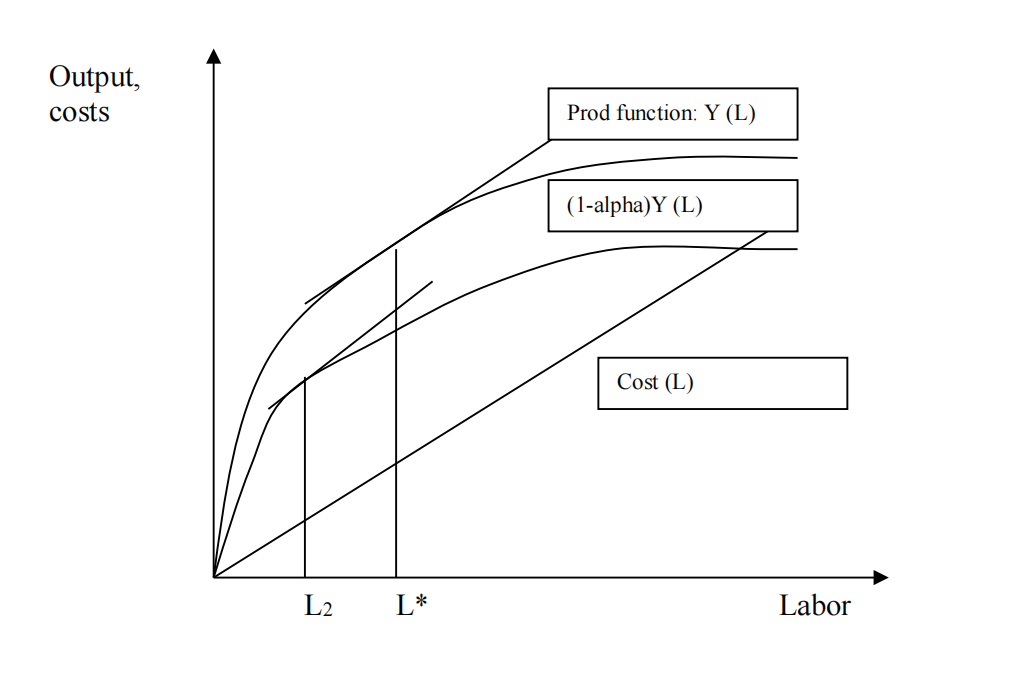
If the farmer’s share is 50% then his “returns” is 50% of the total production function. The farmer supplies labor effort by comparing his personal marginal returns to labor to labor costs. His

optimal labor effort is L2. Farmer maximizes his surplus, not the total surplus from production. Agent is partially insured against risk  less incentive to supply effort/labor because farmer only

gets fraction of any extra output.

In a Fixed Rent Contract, the tenant’s labor returns looks like the following:

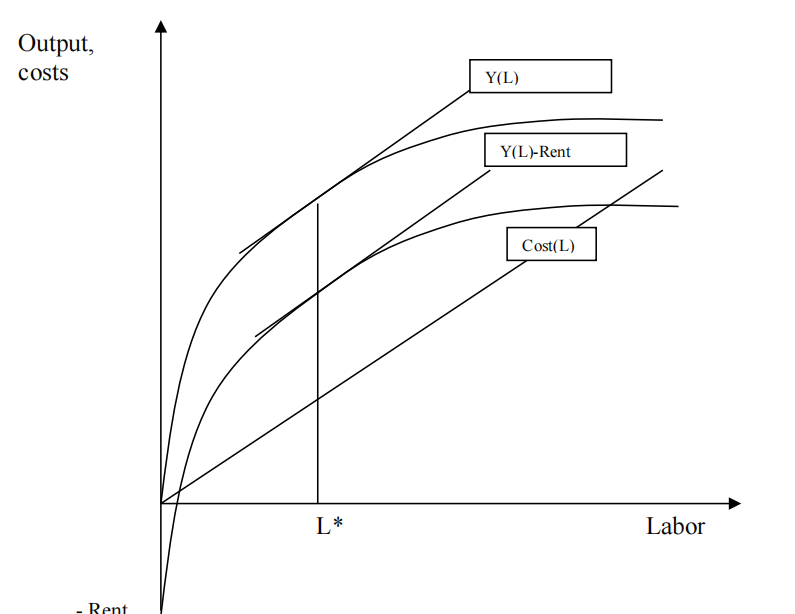
The function depicting the farmer’s return is a parallel shift down. The vertical difference between the two functions is the amount of the fixed rent. Labor supply stays optimal because tenant gets 100% of any extra ouput.

Empirically, what do we find? Do sharecropped farms have lower yield than fixed rent farms?  How do we test this theory we just developed?(Assuming costs are same across both renters and

sharecroppers.)

- Get data on yields on sharecropped land and on owned land or fixed rent land. Compare the yields.

What is the problem with this approach? If you find that owned land has higher yield than sharecropped land, can you automatically conclude that the farmers who sharecropped did not put in as much effort?

No, because people who own land may have better access to working capital than poor farmers who have to sharecrop (b/c have collateral). This may be the reason why yields vary. Solution: control for capital.  发展经济学代写

However, there may be other differences between sharecroppers and landowners. The cleanest way to test the theory is to find some farmers who cultivate some of their own land, and also

sharecrop (maybe during different seasons). Compare the yield across the two plots for the same farmer.

Result: Output per acre significantly higher for owned land than for sharecropped land

Land Tenancy, Risk Aversion and Insurance.

Why would we expect to see sharecropping if it is inefficient at maximizing econ surplus?

How do we measure risk aversion? How can you compare the extent of risk aversion across two different people?

A person is risk averse if she prefers a certain (known, deterministic) sum of money $ X to a lottery with the same expected value $ X.

e.g.

option A: get $ 500

option B: get $ 0 if heads, $ 1000 if tails

keep changing $ 500 in option A. Lower it to $ 490, $ 450 and so forth.  发展经济学代写

Comparing Riskiness of Fixed Rent to Sharecropping

FR: Suppose tenant pays rent R to landlord. Abstract from unobserved effort issues. Assume some fixed amount of labor and other inputs is being applied to the land.

Consider a situation where landowner is wealthy and tenant is poor. Reasonable to assume that tenant is risk-averse and compare with with landowner (who is less risk-averse because he probably has other assets, can diversify, etc.). Assume landowner is risk-neutral.

Output is uncertain. Two states of the world: Good and Bad. Output is G in good state, B in bad state. G>B. Probability of good state: p. Probability of bad state: 1-p.  发展经济学代写

Expected Output= EV= pG + (1-p)B

Tenant gets G-R in good state, B-R in bad state. Expected return to tenant:

p(G-R) + (1-p)(B-R) = EV-R

Landowner gets R for sure.

Now imagine replacing rental contract with sharecropping contract. Where the share is chosen to provide the same expected return to the landlord, R, as before.

Sharecropping: Let s equal the share accruing to the landlord. Expected return to landlord:  发展经济学代写

psG + (1-p)sB

If the landlord is risk neutral, which sharecropping contract is equivalent to the fixed rent contract,what is the value of share s?

It’s the one where the expected returns to the landlord is the same:

psG + (1-p)sB = R

or, s = R / [pG + (1-p)B] = R/EV

Expected return to tenant also the same across the two contractual modes.

(1-s)EV = ((EV-R)/EV)EV = EV-R = p(G-R) + (1-p)(B-R)

The landowner is risk-neutral, so he doesn’t care which contract they use, but tenant is risk averse, so we have to figure out which contract he prefers.  发展经济学代写

Compare tenant’s returns under the two contracts in the good state:

Sharecropping minus FR:

(1-s)G – (G-R) = R –sG = R - GR / [pG + (1-p)B] < 0.

(You can see that R- GR / [pG + (1-p)B] < 0 by multiplying R by G/G = G / [pG + (1-p)G]:

R=GR / [pG + (1-p)G] < GR / [pG + (1-p)B] since G>B.)

Tenant gets less in the good state under the sharecropping contract than under FR.

Since overall expected return to the tenant is the same under both contracts, it must be the case that Tenant gets more in the bad state under the sharecropping contract than under FR. Sharecropping and Fixed-rent contracts are like 2 projects with the same expected returns,  but where the sharecropping contract has a smaller “spread” of returns.

So if the tenant is risk-averse, then he would prefer the sharecropping contract over the  fixed-rent contract. What does this mean for the landowner? The landlord can cut the tenant’s share a bit more so that the tenant still prefers the sharecropping contract to fixed-rent. Now the landlord, who we assumed was risk-neutral, enjoys a larger payoff with sharecropping, so he is happier with this arrangement too.  发展经济学代写

Why stop at sharecropping? Risk-averse tenant will prefer a fixed wage (income) contract equal to EV of sharectopping return, so much so, that the landlord could cut his wage a little bit and the

tenant would still prefer it. Why isn’t this a better way to share risk between landlord and tenant?

(1) Landlord now bears all risk. If landlord is at all risk-averse (even though he is likely to be less risk-averse than the tenant), then an intermediate outcome where risk is shared (sharecropping contract) will be preferred.

(2) Wage solution faces incentive problem. The lower the share afforded to the tenant, the

weaker are his incentives to supply effort. Tension between need to insure farmer against risk and the need to provide him with incentives.  发展经济学代写

Landlord will offer contract to balance insurance and incentives, but full efficiency is not reached (since as we have seen fixed rent is socially optimal).

更多代写：cs代写    计量经济代考   机器学习代写      r语言代写    经济学发展代写