
Advanced Financial Mathematics Notes
高级金融作业代写 the derivative of the option price with respect to the underlying, called the delta of the option, has to be equal to the number
Feynman-Kac Theorem 高级金融作业代写
Theorem: let X be a diffusion satisfying![]()
Denote by![]()
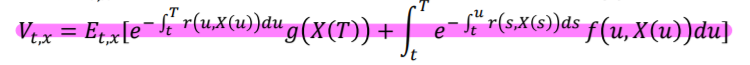
for some given functions r, g, and f . Under technical conditions, function V is the solution to the Feynman-Kac PDF and the boundary conditions
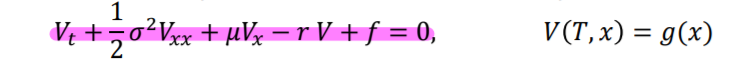
The price of a contingent claim with a random pay-off C at maturity T is computed based on Expectation Formula
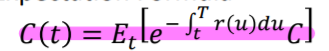
The zero-coupon T -bond that pays 1 dollar at time T has the price
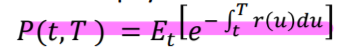
Application of Feynman-Kac![]()
• C: a contingent claim
• Then,
![]()
Black Scholes Equation
• Consider an option with a payoff g(S(T )).The price at time t of this option is given by C(t, S(t)), where function C is a solution to the Black-Scholes PDE and the boundary condition
![]()
Proof 高级金融作业代写

delta of an option
![]() is called delta of an option
is called delta of an option
the derivative of the option price with respect to the underlying, called the delta of the option, has to be equal to the number of shares of stock held by the replicating portfolio.
 更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 霍普学院代写
更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 霍普学院代写




发表回复
要发表评论,您必须先登录。