ECE5606 Stochastic Signals and Systems
随机信号作业代写 Perform the spectral factorization and determine the pulse transfer function of a stable system such that the output has the spectral
Let {u(t), t ∈ T} and {y(t), t ∈ T} be stochastic processes related through the equation 随机信号作业代写
y(t) + a(t − 1)y(t − 1) = u(t)
show that
Ruy(s, t) + a(t − 1)Ruy(s, t − 1) = Ru(s, t)
Ryu(s, t) + a(s − 1)Ryu(s − 1, t) = Ru(s, t)
A stationary discrete time stochastic process has the spectral density
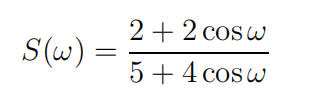
Perform the spectral factorization and determine the pulse transfer function of a stable system such that the output has the spectral density S when the input
is white noise.
Consider a normal stationary process y(t) which is generated by 随机信号作业代写
y(t) = x1(t) + x2(t)
where
x1(t + 1) = − ax1(t) + v1(t) (1)
x2(t + 1) = − bx2(t) + v2(t) (2)
where {v1(t)} and {v2(t)} are sequences of independent normal (0, σ1) respec tively (0, σ2) stochastic variables. Show that a stochastic process with the same
spectral density can be represented by
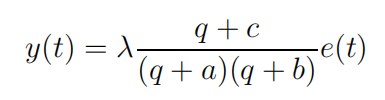
where q is the shift operator (qy(t) = y(t + 1)), the same as z in the notes, and {e(t)} is a sequence of independent normal (0, 1) stochastic variables. Deter
mine the parameters λ and c. 随机信号作业代写
Consider the moving average process
y(t) = e(t)+4e(t − 1)
where {e(t), t = ..., −1, 0, 1, ...} is a sequence of independent normal (0, 1) ran dom variables. Show that a process with the same spectral density can be generated by
y(t) = λ[ (t) + c(t − 1)]
where { (t), t = ..., −1, 0, 1, ...} is a sequence of independent normal (0, 1) stochastic variables and |c| < 1. Furthermore, determine c and λ.





发表回复
要发表评论,您必须先登录。