MAT1841 Continuous Mathematics for Computer Science
计算机科学连续数学代写 The standard penalty of 10% of the total mark per day will apply for late work. Show your working. You are required to
Assignment 3 计算机科学连续数学代写
The assignment is to be submitted via MOODLE via 11:55 pm AEDT Friday 14 October 2021. See the instructions under the assessment tab on MOODLE. Be sure to press the “submit assignment” button to complete the submission. You must submit a single PDF document no larger than 100MB in size. It’s the student’s responsibility to ensure that the file is not corrupted.
Assignment 3 is worth 10% of the final mark. There are four questions.
The standard penalty of 10% of the total mark per day will apply for late work. Show your working. You are required to clearly explain your steps in both English and mathematical expressions. Most of the marks will be allocated for clear working and explanations. A mathematical writing guide is available on Moodle.
- Compute the first four non-zero terms in the Taylor series for the following functions centred about the specified point ?. [5 + 5 = 10 marks]
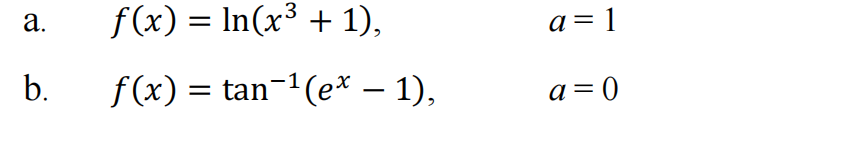
Calculate the three cubic splines that pass through the four points 计算机科学连续数学代写
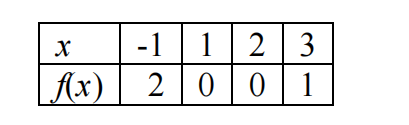
with the second derivatives set equal to zero at the two endpoints. Using a software package, graph the three cubic splines over the domain ? ∈ [−1, 3]. [16 + 2 = 18 marks]
- Use integration by parts to calculate the following integrals. [4 + 4 = 8 marks]
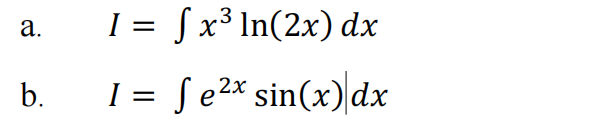
- Consider the area bounded by the two functions ? = (?! − 5?% + 4?)/5 and ? = ?% − 4? over the domain 0 ≤ ? ≤ 4. [2 + 4 + 4 + 4 = 14 marks]
- Sketch these two curves, noting the area bounded between them.
- Use the Fundamental Theorem of Calculus to calculate the area bounded between the two curves. 计算机科学连续数学代写
- Approximate the area between the curves using the Trapezoidal rule with n = 4.
- Approximate the area between the curves using the Trapezoidal rule with n = 8.

更多代写:cs代写 经济代考 会计代写 计算机科学代写 Simpletense怎么样




发表回复
要发表评论,您必须先登录。