Dynamic Programming I of IV
算法algorithm作业代写 Using the recursion idea of findHill algorithm we built in Part (a), we can solve the 2d version of the question by splitting
Question 1 算法algorithm作业代写
To make the resulting graph acyclic, the remaining graph must be a tree after the selected edges removed. Since the total weight of the original graph is known, and the edge set to be removed must have a minimum weight, then the resulting tree would be the maximum spanning tree. Therefore we can modify the Prim’s algorithm in the following manner to find this tree first:
PrimMaxSpanTree(G=(V,E)):
Step 1: Pick any element v from V, set and
Step 2: Find the edge with maximum weight such that . Add to .
Step 3: If , then return A.
Now to find the edge set to be removed, we can use the following routine:
FindRemoveEdges(G=(V,E)):
Step 1: A = PrimMaxSpanTree(G)
Step 2: Let , for every edge e in E:
If , then add e to R
Step 3: return R
The Prim’s algorithm would run in time. The final loop takes time. Therefore the total time complexity is .
Question 2
- Note that the question only asked us to find “a hill” instead of “all hills”, we may use divide and conquer to quickly divide the whole task into smaller pieces to achieve sublinear time. Suppose we guess the middle element in the 1d array is the “hill”, if the two conditions were all tested correct, then we find a hill and return it. If not, assume that the right neighbor is bigger (), we claim that there would always be a hill on the right half of the array, to see this:
- For any element from the middle of the array to the right end of the array to “not be a hill”, they must now all be smaller than their right neighbor.
Otherwise we will have a hill instantly.
- But the element on the rightmost position of the array has no right neighbor. Therefore it is the biggest element from middle element to the right end of the array.
- Then the rightmost element would be the hill.
So there would always be a hill on the right half of the array if the right neighbor is bigger. Similarly, if , then there will always be a hill in the left half of the array as well. The algorithm we designed is shown below:
findHill(A):
Let rounded up if length of T is odd.
Test
If true, then:
Test
If true, then return and its position
Else:
findHill()
Else:
findHill()
Time complexity of the algorithm is , assume that the algorithm searched T times till a hill is found, we know that because by each test of hill condition, the array was cut into two halves. So for an array with length n, we need to test times.
- Using the recursion idea of findHill algorithm we built in Part (a), we can solve the 2d version of the question by splitting the matrix into n column arrays with length n. Starting from the middle column of the matrix, we can always find “a hill” of this column. Now suppose this hill of the column is also larger than its neighbors from the left and right column, we have the hill for the matrix and are done.
If not, suppose that the right column neighbor is larger than the column hill, then we would have a similar claim
Question 4 算法algorithm作业代写
- The Forest-Verify problem belongs to NP because it has a polynomial time verifier for every instance :
Verify(x):
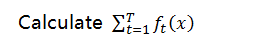
Return true the sum is nonnegative. Returns false otherwise.
Because each tree would take no more than steps to decide, (note ). And there is T trees, so the total number of steps to verify an instance takes no more than steps. is a polynomial time verifier. So Forest-Verify problem belongs to NP.
- A single decision tree can be converted into a 3-SAT problem using the following procedure, take one of the given tree for example:

Step 1: write out all the path from root to all leaves that leads to output of +1 in DNF:
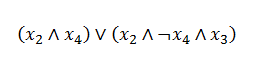
Step 2: Convert the DNF formula to CNF with the following
 更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 英文报告代写怎么找
更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 英文报告代写怎么找




发表回复
要发表评论,您必须先登录。