Spring 2018 EC 399 Final Exam (Version A)
电子商务作业代写 Suppose that both players have Rawsian social preferences. That is, each player cares about the minimum payoff of the two players.
Problem 1 (20 pts) 电子商务作业代写
Suppose Kate’s value function is given by v(x) = √x for gains (x ≥ 0) and v(x) = −√−2x for losses (x < 0). Kate is facing the choice between option (A) a sure amount $250 and option (B) a gamble which gives Kate $400 with probability 0.75 and $0 with probability 0.25.
- If Kate uses her current endowment ($0) as her reference point, what are the values of the two options? Which option would Kate prefer? Draw the graph of Kate’s value function, point out the values corresponding to the two options on the graph. (10 pts)
- If Kate uses Option A’s outcome as her reference point, what are the values of the two op- tions? Which option would Kate prefer? Draw the graph of Kate’s value function, point out the values corresponding to the two options on the graph. (10 pts)
Problem 2 (20 pts)
What is the total value of Jim if he integrates both losses? What is the total value of Jim if he separates the two losses? From Jim’s view, should he integrate or separate? (10 pts)Suppose Jim first lost $20000 in the stock market two days ago. Then he lost another $8000 in the stock market again today. Assume that Jim’s value function is given by v(x) = x/4 when x ≥ 0; v(x) = −2√−x/2 when x < 0.
- Please draw the graph that illustrates the values corresponding to Jim’s two losses and the integration of the two (10 pts)
Problem 3 (40pts) 电子商务作业代写
Assume that Tony is going to watch one movie. He can either go to Movie A in week 1, or go to Movie B in week 2, or go to Movie C in week 3. Suppose Movie A gives him a utility of 5, Movie B gives him a utility of 7, Movie C gives him a utility of 10.
- Suppose that Tony is an exponential discounter with parameter δ = 0. Which option would he eventually choose? Try to depict the three options on a graph and draw the different time indifference curves that go through them. (16 pts)
- Suppose that Tony is a naive hyperbolic discounter with parameter δ = 0.9 and β = 0. Which option would he eventually choose? (12 pts)
- Suppose that Tony is a sophisticated hyperbolic discounter with parameter δ = 0.9 and β = 0. Which option would he eventually choose? (12 pts)
Problem 4 (40pts)
- Conisder the following game table. Numbers in the table represent monetary
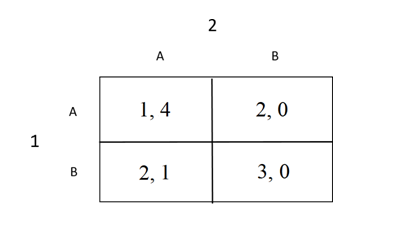
1a) Suppose both players only care about monterary payoffs. Find if any player has a strictly dom- inated strategy. What is the prediction of the game if both players never play strictly dominated strategies? (5 pts)
1b) Suppose that player 1 has altruistic preferences with an altruistic level of 0.5. That is, she cares about her own monetary payoff plus half of player 2’s monetary payoff. Player 2 has spiteful preferences with a spiteful level of 0.5. That is, he cares about his own monetary payoff minus half of player 1’s monetary payoff. Draw the corresponding new game table, circle the best responses and find the pure Nash equilibria. (15pts)
- Conisder the following game tree. Numbers in the tree represent monetary
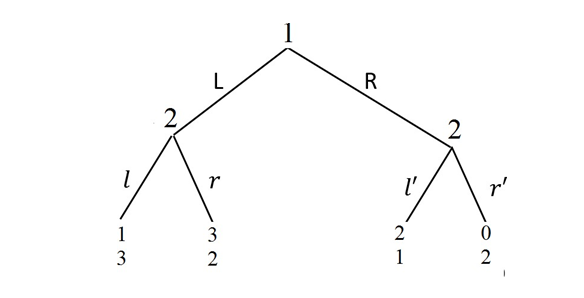
2a) Suppose both players only care about monterary payoffs. Find the subgame perfect equilibria. (5 pts)
2b) Suppose that both players have Rawsian social preferences. That is, each player cares about the minimum payoff of the two players. Draw the corresponding new game tree, find the subgame perfect equilibria. (15 pts)
Problem 5 (20pts) 电子商务作业代写
- Suppose Bella is presented with a box filled with 100 colored tickets. Bella knows that 80 of them are black, 15 of them are blue, 5 of them are green. Suppose Bella is invited to randomly draw a ticket from the She is offered the following gambles: (A) regardless of the color of the ticket, she gets $10. (B) If the ticket is black, she gets $20, if the ticket is blue, she gets 0, if the ticket is green, she gets 10. (C) If the ticket is black, she gets $20. Otherwise, she gets $0. (D) If the ticket is either black or blue, she gets $10. Otherwise, she gets $0.
Draw a table for the four gambles. Point out which column corresponds to “sure thing.” Sup- pose Bella prefers (B) to (A) and she prefers (C) to (D). Does she violates the sure-thing principle? (10 pts)
- According to the peak-end rule, which of the following episodes would a decision maker choose from? Explain. (10 pts)

Problem 6 (10pts)
Suppose Player 1 is a male player, player 2 is a female player.
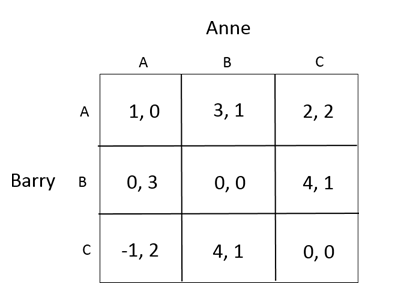
Assume that player 1 is a level-3 player, player 2 is also a level-3 player. Suppose that in the real world, level-0 male player tends to choose A, level-0 female player tends to choose C. What is the prediction of the game? Explain.
 更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 经济Final Exam代考
更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 经济Final Exam代考




发表回复
要发表评论,您必须先登录。