ENVE4403 Assignment 1
环境工程学代写 A vertical belt moves upwards and draws a thin film of fluid out of a tank. The fluid film maintains a constant thickness (h) along
Question 1 [5 marks] 环境工程学代写
A vertical belt moves upwards and draws a thin film of fluid out of a tank. The fluid film maintains a constant thickness (h) along the belt. Assume the belt is very wide, and moves steadily at speed Wbelt.
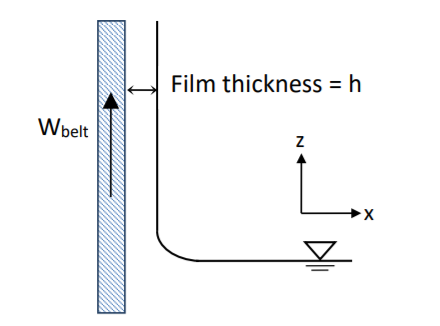
(a) If the ambient air is stationary, find the minimum belt velocity that has all the fluid in the film moving upwards. [3 marks]
(b) For the value of the belt velocity in (a), sketch the velocity profile in the film, providing as much detail as possible. [1 mark]
(c) If the belt is 100 cm tall and 50 cm wide (into the page), what is the power required to drive the belt at this speed? [1 mark]
Question 2 [3 marks] 环境工程学代写
So far in class we have touched upon three dimensionless parameters: the Reynolds number, the Rossby number and the Ekman number. Write out the full conservation of momentum
equation in the x-direction, and show how each of these parameters represents the ratios of scales of terms in the equation. [2 marks] Explain in your own words why consideration of the magnitude of dimensionless parameters is important in environmental fluid mechanics. [1 mark]
Question 3 [7 marks]
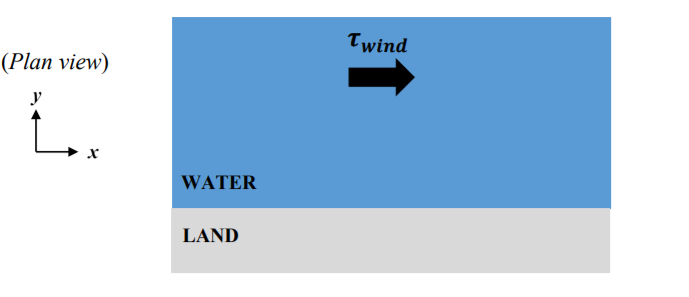
In practice problem 4, we looked at the wind-stress-driven oceanic flow generated by a large-scale high pressure system.

When the wind blows entirely in the x-direction (as in the figure above), there is a constant wind stress vector (??????????, 0). It has been proposed that a solution to the resulting steady-state fluid motion in the ocean is:
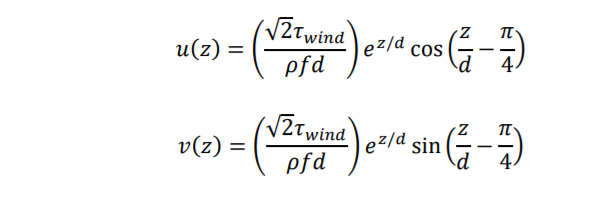
where the length scale![]() is known as the ‘Ekman layer depth’.
is known as the ‘Ekman layer depth’.
(a) Verify that this is a valid solution to the equations of motion and that it satisfies the relevant boundary conditions. [2 marks]
(b) Consider this phenomenon off the coast of San Francisco, California. A typical quantification of the wind stress on the ocean is 0.001??????10
2 , where ??10 is the wind speed (at a height of 10 m) and ???? is the density of air. For a wind speed of 10 m/s, plot the velocity vector in the ocean, and its variation over depth. Use this plot to explain why this flow is typically called the ‘Ekman spiral’. [2 marks]
(c) Calculate the flux of water per unit length in both the x and y directions as a result of this wind stress:
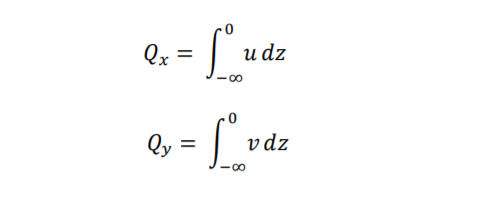
(Qx is the total flow of water in the x-direction per unit distance offshore. And Qy is the total flow of water in the y-direction per unit length of coastline). [2 marks]
Hint: While it is tempting to just substitute the provided expressions for u(z) and v(z) into these integrals. The maths will be cumbersome. Try making substitutions from your simplified
equations of motion – it will be worth it!
(d) What is the direction of the total water flux relative to the forcing wind stress? [0.5 marks]
(e) How would your plot in (b) change if the flow was turbulent? [0.5 marks]

更多代写:HomeWork cs作业 Econ代考 postgreSQL代写 Philosophy论文代写 英国代写 argumentative essay论文代写




发表回复
要发表评论,您必须先登录。