EECS 126: Probability and Random Processes
概率和随机过程代写 Three frogs are playing near a pond. When they are in the sun they get too hot and jump in the lake at rate 1. When they are in
Reversible Markov Chains 概率和随机过程代写
Let (Xn)n∈N be an irreducible Markov chain on a finite set X , with stationary distribution π and transition matrix P . The graph associated with the Markov chain is formed by taking the transition diagram of the Markov chain, removing the directions on the edges (making the
graph undirected), removing self-loops, and removing duplicate edges. Show that if the graph associated with the Markov chain is a tree, then the Markov chain is reversible.
Hint : To solve this problem, try induction on the size of X :
- Use the fact that every tree has a leaf node x connected to only one neighbor y, and show that detailed balance holds for the edge (x, y) connecting the leaf with its single neighbor.
- Then, argue that if you remove the leaf x from the Markov chain and increase the probability of a self-transition at state y by P (y, x), then the stationary distribution of the original chain (when restricted to X \ {x}) is the stationary distribution for the new chain, and use this to conclude the inductive
Bus Arrivals at Cory Hall
Starting at time 0, the 52 line makes stops at Cory Hall according to a Poisson process of rate λ. Students arrive at the stop according to an independent Poisson process of rate µ. Every time the bus arrives, all students waiting get on.
- Given that the interarrival time between bus i − 1 and bus i is x, find the distribution for the number of students entering the ith bus. (Here, x is a given number, not a random )
- Given that a bus arrived at 9:30 AM, find the distribution for the number of students that will get on the next
- Find the distribution of the number of students getting on the next bus to arrive after 9:30 AM, assuming that time 0 was infinitely far in the
Frogs 概率和随机过程代写
Three frogs are playing near a pond. When they are in the sun they get too hot and jump in the lake at rate 1. When they are in the lake they get too cold and jump onto the land at rate 2. The rates here refer to the rate in exponential distribution. Let Xt be the number of frogs in the sun at time t ≥ 0.
- Find the stationary distribution for (Xt)t≥0.
- Check the answer to (a) by noting that the three frogs are independent two-state Markov
Taxi Queue
Empty taxis pass by a street corner according to a Poisson process of rate two per minute and pick up a passenger if one is waiting there. Passengers arrive at the street corner according to a Poisson process of rate one per minute and wait for a taxi only if there are less than four persons waiting; otherwise they leave and never return. John arrives at the street corner at a given time. Find his expected waiting time, given that he joins the queue. Assume that the process is in steady state.
M/M/2 Queue 概率和随机过程代写
A queue has Poisson arrivals with rate λ. It has two servers that work in parallel. When there are at least two customers in the queue, two are being served. When there is only one customer, only one server is active. The service times are i.i.d. exponential random variables with rate µ. Let X(t) be the number of customers either in the queue or in service at time t.
- Argue that the process (X(t), t ≥ 0) is a Markov
- Draw the state transition
- Find the range of values of µ for which the Markov chain is positive-recurrent and for this range of values calculate the stationary distribution of the Markov
Jukes-Cantor Model
In this question we consider a CTMC model for the evolution of DNA over time. Consider a CTMC (Xt)t≥0 on the states X := {A, C, tt, T } with transition rate matrix
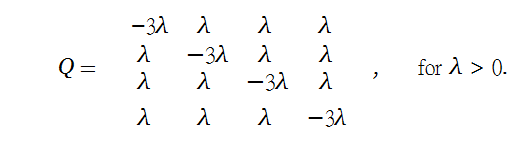
For x, y ∈ X , what is Pt(x, y) := P(Xt = y | X0 = x)? What happens as t → ∞?

Figure 1: All edges in the rate diagram have rate λ.


 更多代写:
更多代写:

发表回复
要发表评论,您必须先登录。