CS2230 Computer Science II: Data Structures
Homework 4
Asymptotic Analysis
数据结构分析代写 Your summation should not be overly pessimistic, even when it leads to the same f(N) as another summation. For example,
All of the problems are of the same type as Lab 7 and Lab 8.
See the readings in Asymptotic Analysis for help with these topics.
Goals for this homework
• Use Big-Oh/Theta/Omega notation
• Analyze the running time of iterative and recursive functions
Part 1: Growth rate 数据结构分析代写
- Order the following functions by asymptotic order of growth (lowest to highest)
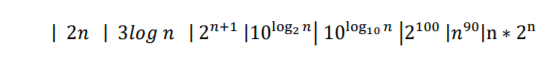
Part 2: Proof and Analysis
- Show that the following statement is true:
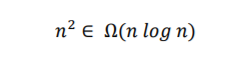
Part 3: Algorithm Analysis
For each problem, please provide
i. Describe the worst-case input (the input that would cause the largest running time)
ii. Summation used to calculate number of steps for the worst case
iii. Explanation of how the code relates to the summation
a. (loops require discussing number of iterations and steps per iteration)
b. (recursion requires a diagram)
iv. A Θ bound
These are the same 4 items found in the lectures and lab.
Your summation should not be overly pessimistic, even when it leads to the same f(N) as another summation. For example,
for (int i=0; i<N; i++) {
for (int k=0; k<i; k++) {
println();
}
}These summations are both in Θ(?2) but the second one better represents the code
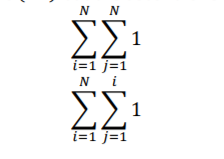
- R(L) is the worst-case running time of foo when called on an array of length L. 数据结构分析代写
static int foo(int[] z) {
int x = z.length;
for (int i=0; i<x/2; i++) {
for (int j=0; j<x; j+=3) {
if (z[i] == 10) {
System.out.println("Hi");
break;
}
}
for (int k=0; k<x; k++) {
System.out.println("Lo");
if (k >= i) {
break;
}
}
}
}
- R(N, M) is the worst-case running time of baz(x, y) when x has length N and y has length M. In this case you are finding an ?(?, ?) such that ?(?, ?) ∈ Θ(?(?, ?)) . ?(?, ?) must include both N and M.
static void baz(int[] x, int[] y) {
for (int i=0; i<x.length; i++) {
for (int j=i; j<y.length; j+=20) {
for (int k=0; k<10; k++) {
if (k < x.length) {
int z = a[k];
a[k] = a[i];
a[i] = z;
}
}
}
}
}Consider this code for the next two problems. 数据结构分析代写
static Integer sum(List a) { if (a.size() == 0) { return 0; } else if (a.size() == 1) { return a.get(0); } else { int leftLen = a.size()/2; int rightLen = a.size() - leftLen; List aLeft = new ______<>(); List aRight = new ______<>(); for (int i=0; i<leftLen; i++) { Integer x = a.get(i); aLeft.add(i, x); } for (int i=0; i<rightLen; i++) { Integer x = a.get(i+leftLen); aRight.add(i, x); } return sum(aLeft) + sum(aRight); } }- R(N) is the worst-case running time of sum when called on a LinkedList of size N (and the two blanks are filled in with LinkedList). As part of iii (the explanation of summation), you must also state your assumptions about the running time of each LinkedList method (including constructor), with justification.
R(N) is the worst-case running time of sum when called on an ArrayList of size N (and the two blanks are filled in with ArrayList). As part of iii (the explanation of summation), you must state your assumptions about the running time of each ArrayList method (including constructor), with justification
 更多代写:计算机作业代写 经济代考 essay代写 AI作业代做 accounting代做
更多代写:计算机作业代写 经济代考 essay代写 AI作业代做 accounting代做




发表回复
要发表评论,您必须先登录。