Math 417: Final Exam
数学Final Exam代考 In this problem we assume that G is an abelian group whose operation is always written as +. Let E(G,+) be the set of all group
Instructions: 数学Final Exam代考
• This is a take-home exam. Please solve the problems and upload your solutions to Moodle.
• The deadline to submit the exam is 11:59pm on Friday, May 14, 2021.
• Please submit your exam in PDF format if at all possible.
• There are 140 points possible on this exam.
• Unlike the homework, collaboration is not permitted on the exam. You are allowed to refer to the textbook, lecture notes, lecture videos, homework solutions on Moodle, your own homework, and any notes that you have made. You may not consult other resources when taking the exam.
• Any questions about the exam should be directed to your instructor.
Problems:
- (10 points) Suppose that G is isomorphic to a semidirect product Z26oαZ5, for some homomorphism α : Z5 → Aut(Z26). Prove that G is necessarily isomorphic to the direct product Z26 ×Z5. 数学Final Exam代考
(15 points) Let p be a prime number, and let n be a positive integer. Let X = (Zp)n be the set of vectors of length n with entries in Zp. The multiplicative group Z×p = Zp \ {0} acts on X by the rule [a]·([x1],..., [xn]) = ([ax1],..., [axn]) Find the number of orbits of this action as a function of p and n, and justify your answer.
(15 points) Prove that, up to isomorphism, there is only one group that has exactly two conjugacy classes.
4. Let G be a group of order pqr , where p,q, r are primes, p < q < r , and pq < r .
(a) (5 points) Prove there is a unique r -Sylow subgroup in G.
(b) (10 points) Prove that G contains a normal subgroup of order qr .
- For any two sets X and Y , we shall write Fun(X,Y ) for the set of all functions from X to Y . Let K be a field. (a) (5 points) Let X be any set. Show that the set Fun(X,K) with the operations given by
(f + g )(λ) = f (λ)+ g (λ) for λ ∈ X
(f · g )(λ) = f (λ)· g (λ) for λ ∈ X
is a ring. Identify explicitly the additive identity and the multiplicative identity in this ring. 数学Final Exam代考
(b) (5 points) Consider the ring Fun(K,K) of all functions from K to itself. Show that the map
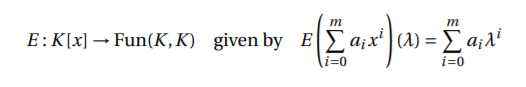
is a unital homomorphism of rings.
(c) (7 points) Suppose K = R. Show that the map E is injective. Hint: See Corollary 1.8.24 in Goodman.
(d) (8 points) Suppose K = Zp where p is prime. Show that the kernel of E is precisely the ideal generated by x p − x. Hint: If you are having trouble seeing why this map is not injective, consider the fact that Fun(Zp,Zp) is a finite set, while Zp[x] is an infinite set.
- (15 points) Let f (x), g (x) ∈ Q[x] be nonzero polynomials with coefficients in Q. Show that gcd(f , g ) = 1 if and only if f (x) and g (x) have no common roots in C. Hint 1: You may use the fact that C is algebraically closed: any nonconstant polynomial with coefficients in C has a root in C. Hint 2: There exist a,b ∈ Q[x] so that gcd(f , g ) = a f +bg ).
7. In this problem A denotes a commutative ring with multiplicative identity. 数学Final Exam代考
(a) (8 points) Suppose that A is an integral domain, and that A has finitely many elements. Show that A is a field. Hint: Show that for any nonzero a ∈ A, the multiplication map fromA to A defined by b 7→ a · b is injective. What do you know about injective maps from a finite set to itself?
(b) (7 points) Let A be any commutative ring with multiplicative identity that has finitely many elements. Show that any prime ideal in A is maximal.
- In this problem we assume that G is an abelian group whose operation is always written as +. Let E(G,+) be the set of all group homomorphisms from (G,+) to (G,+). Define the sum ϕ+ψ of two homomorphisms ϕ,ψ ∈ E(G,+) by the formula
(ϕ+ψ)(x) = ϕ(x)+ψ(x),
where on the right-hand side the addition takes place in the abelian group (G,+). Define the product of two homomorphisms by the formula
(ϕψ)(x) = (ϕ◦ψ)(x) = ϕ(ψ(x))
(a) (10 points) Prove that the addition of two elements of E(G,+) is indeed an element of E(G,+), and verify that E(G,+) with the operations defined above is a unital ring.
(b) (10 points) Consider the case where (G,+) = (Z × Z,+). Prove that the ring E(Z × Z,+) is isomorphic to the ring of 2×2 matrices with integer entries.
(c) (10 points) Consider the case where (G,+) = (Q,+). Prove that the ring E(Q,+) is isomorphic to the ring (Q,+,·). 数学Final Exam代考


 更多代写:
更多代写:

发表回复
要发表评论,您必须先登录。