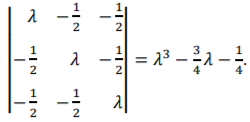
homogeneous linear system
数学齐次线性系统代写 For this to hold for all real values of ?, the coefficients corresponding to the same powers of ? on both sides must match
(a) The vector equation ?(−3,0,4) + ?(5, −1,2) + ?(1,1,3) = (0,0,0) can be rewritten as a homogeneous linear system by equating the corresponding components on both sides 数学齐次线性系统代写
−3? + 5? + 1? = 0
0? − 1? + 1? = 0
4? + 2? + 3? = 0
The augmented matrix of this system has the reduced row echelon form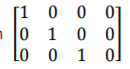
therefore the system has only the trivial solution ? = ? = ? = 0. We conclude that the
given set of vectors is linearly independent.
(b) A set of 4 vectors in ?3 must be linearly dependent by Theorem 4.3.3.
4. (a) The terms in the equation ?(2 − ? + 4?2) + ?(3 + 6? + 2?2) + ?(2 + 10? − 4?2) = 0 can be grouped according to the powers of
? (2? + 3? + 2?) + (−? + 6? + 10?)? + (4? + 2? − 4?)?2 = 0 + 0? + 0?2
For this to hold for all real values of ?, the coefficients corresponding to the same powers of ? on both sides must match, which leads to the homogeneous linear system
2? + 3? + 2? = 0
−? + 6? + 10? = 0
4? + 2? − 4? = 0
The augmented matrix of this system has the reduced row echelon form therefore the system has only the trivial solution ? = ? = ? = 0. We conclude that the
therefore the system has only the trivial solution ? = ? = ? = 0. We conclude that the
given set of vectors in ?2 is linearly independent.
(b) The terms in the equation
?(1 + 3? + 3?2) + ?(? + 4?2) + ?(5 + 6? + 3?2) + ?(7 + 2? − ?2) = 0
can be grouped according to the powers of ?
(? + 5? + 7?) + (3? + ? + 6? + 2?)? + (3? + 4? + 3? − ?)?2 = 0 + 0? + 0?2
For this to hold for all real values of ?, the coefficients corresponding to the same powers of ? on both sides must match, which leads to the homogeneous linear system
? + 5? + 7? = 0
3? + ? + 6? + 2? = 0
3? + 4? + 3? − ? = 0
The augmented matrix of this system has the reduced row echelon form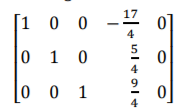 therefore a general solution of the system is
therefore a general solution of the system is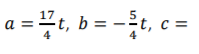
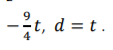
Since the system has nontrivial solutions, the given set of vectors is linearly dependent.
5. (a) The matrix equation 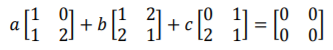 can be rewritten as a homogeneous linear system 数学齐次线性系统代写
can be rewritten as a homogeneous linear system 数学齐次线性系统代写
1? + 1? + 0? = 0
0? + 2? + 1? = 0
1? + 2? + 2? = 0
2? + 1? + 1? = 0
The augmented matrix of this system has the reduced row echelon form  therefore the system has only the trivial solution ? = ? = ? = 0. We conclude that the
therefore the system has only the trivial solution ? = ? = ? = 0. We conclude that the
given matrices are linearly independent.
(b) By inspection, the matrix equation![]()
![]() has only the trivial solution ? = ? = ? = 0. We conclude that the given
has only the trivial solution ? = ? = ? = 0. We conclude that the given
matrices are linearly independent.
- By inspection, when
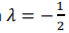 , the vectors become linearly dependent (since they all become equal). We proceed to find the remaining values of ?.
, the vectors become linearly dependent (since they all become equal). We proceed to find the remaining values of ?.
The vector equation ![]() can be rewritten as a homogeneous linear system by equating the corresponding components on both sides
can be rewritten as a homogeneous linear system by equating the corresponding components on both sides
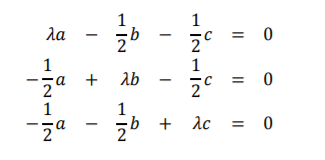
The determinant of the coefficient matrix is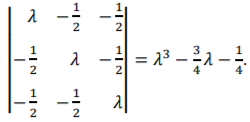 This determinant equals zero for all ? values for which the vectors are linearly dependent. Since we already know that
This determinant equals zero for all ? values for which the vectors are linearly dependent. Since we already know that
![]() is one of those values, we can divide
is one of those values, we can divide![]() to obtain
to obtain
![]()
We conclude that the vectors form a linearly dependent set for![]()
- Three vectors in ?3 lie in a plane if and only if they are linearly dependent when they have their initial points at the origin. (See the discussion following Example 6.)
(a) After the three vectors are moved so that their initial points are at the origin, the resulting vectors do not lie on the same plane. Hence these vectors are linearly independent.
(b) After the three vectors are moved so that their initial points are at the origin, the resulting vectors lie on the same plane. Hence these vectors are linearly dependent.
 更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 劳动经济学作业代写
更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 劳动经济学作业代写




发表回复
要发表评论,您必须先登录。