MAT301 Week 7 Exercises
数学群论代考 The universal property of π is useful for defining homomorphisms out of G/N. For each homomorphism φ : G → H with N ≤ ker φ
Recall that if G is a group we write H E G to express that “H is a normal subgroup of G”.
1 Examples of normal subgroups 数学群论代考
Exercise 1. Determine the normal subgroups of S3.
Exercise 2. Prove that the subgroup hri of rotations in Dn is a normal subgroup of dn.
Exercise 3. Prove that H = {id,(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)} is a normal subgroup of A4. (It can be proved that H is the only proper and non-trivial subgroup of A4.)
Exercise 4 (A non-abelian group for which all subgroups are normal). Prove that every subgroup of Q8 is a normal. 数学群论代考
Exercise 5 (Subgroups of index 2 are normal). Let G be a group and let H be a subgroup of G of index 2 in G. Using the fact that there is only one left coset of H in G that is not equal to H and that there is only one right coset of H in G that is not equal to H, prove that H E G.
Exercise 6. Let G be a group and let H E G with |H| = 2. Prove that H ⊆ Z(G). (This exercise is included here because the preceding exercise might give you a hint for its solution and because it will help you with the next exercise.)
Exercise 7. Determine all normal subgroups of Dn of order 2.
Exercise 8 (The outer automorphism group). Let G be a group. For each g ∈ G, let Int(g) ∈ Aut(G) denote conjugation by g, i.e. for all x ∈ G we have Int(g)(x) = gxg−1 . Let Int(G) = {Int(g) : g ∈ G}, which we recall is called the inner automrophism group of G and its elements are called inner automorphisms of G. Prove that Int(G) E Aut(G). (The quotient group Out(G) = Aut(G)/ Int(G) is called the outer automorphism group of G even though its elements are not actually automorphisms of G.)
Exercise 9 (The centraliser of a normal subgroup). Let G be a group and let H E G. 数学群论代考
1. Prove that CG(H) E G.
2. Prove that G/CG(H) is isomorphic to a subgroup of Aut(H).
Exercise 10 (A5 is simple). Assuming that every non-trivial normal subgroup of A5 contains a 3-cycle (which you will prove in Assignment 4), prove that there does not exist a proper and non-trivial normal subgroup of A5. (A non-trivial group that does not have a proper and non-trivial normal subgroup is called a simple group. Therefore A5 is simple. It can be proved that for all n ≥ 5, every non-trivial normal subgroup of An contains a 3-cycle, and consequently that An is simple.)
2 Basic properties and constructions 数学群论代考
Exercise 11. Let G be a group and let H E G. Using the fact that G → G/H, g 7→ gH is a surjectivehomomorphism, prove that a quotient group of an abelian (resp. cyclic) group is abelian (resp. cyclic).
Exercise 12. Let G be a group.
1. Prove that if K ≤ H ≤ G and K E G, then K E H.
2. Prove that if H, K ≤ G and K E G, then K ∩ H E H
2.1 Intersections
Exercise 13 (Arbitrary intersections of normal subgroups are normal). Let G be a group and let {Hi}i∈I be an arbitrary set of normal subgroups of G. Prove that Ti∈I Hi is a normal subgroup of G.
Exercise 14 (The normal subgroup generated by a set). Let G be a group and let S be a subset of G. Define the normal subgroup of G generated by S (or normal closure of S in G) to be the subgroup
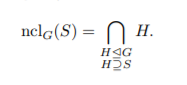
- Prove that nclG(S) is the the unique minimal normal subgroup of G that contains S, that is, nclG(S) is the unique subgroup of G with the following properties: (i) nclG(S) is a normal subgroup of G containing S; (ii) if N is a normal subgroup of G containing S, then nclG(S) ⊆ N. For each subset T of G, define GT to be the set of conjugates of T in G, that is, GT = {gtg−1 : g ∈ G}.
Prove that nclG(S) = h GSi, the subgroup of G generated by GS. 数学群论代考
2.2 Orders 数学群论代考
Exercise 15. Let G be a group, let H E G, and let a ∈ G.
1. Complete the following sentence. The order of aH in G/H is infinite if and only if a n ... for all positive integers n.
2. Suppose that aH has finite order in G/H. Complete the following sentence. The order of aH in G/H is the smallest positive integer n such that a n ... . 数学群论代考
Exercise 16. Let G be an abelian group and let H be the subgroup of G consisting of all elements of G of finite order. Prove that every non-identity element of G/H has finite order.
Exercise 17. Let G be a group, let H be a finite normal subgroup of G, and let n ∈ Z>0. Prove that if G/H has an element of order n, then G has an element of order n. (Note that if G = Z, H = 2Z, then G/H = Z/2Z has an element of order 2, but G = Z does not. Therefore the assumption that H is finite cannot be dropped.)
2.3 Subgroups of subgroups and characteristic subgroups
Exercise 18 (Normality is not transitive, i.e. K E H E G =6⇒ K E G)). Give an example of a group G, a normal subgroup H of G, and a normal subgroup K of G such that K is not a normal subgroup of G.
Exercise 19 (Characteristic subgroups). Let G be a group. A subgroup H ≤ G is said to be a characteristic subgroup of G if for all φ ∈ Aut(H) we have φ(H) = H. We write H char G to express that H is a characteristic subgroup of G. 数学群论代考
- Prove that H = {id,(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)} is a characteristic subgroup of A4.
- Prove that every characteristic subgroup of G is a normal subgroup of G.
- Prove that a subgroup H of G is a characteristic subgroup of G if and only if for all φ ∈ Aut(G) we have φ(H) ≤ H.
- Prove that Z(G) is a characteristic subgroup of G.
- Prove that if K char H char G, then K char G, i.e. being a characteristic subgroup is a transitive relation
- Prove that if K char H E G, then K E G.
Exercise 20. Let G be a group and let N be a cyclic normal subgroup of G. Prove that if H ≤ N, then H E G. 数学群论代考
Exercise 21 (The derived or commutator subgroup). Let G be a group. Define G0 to be the subgroup of G generated by the set of commutators of elements of G. That is,
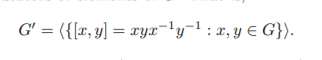
The subgroup G0 is called the derived subgroup (or commutator subgroup) of G.
1. Prove that G0 is a characteristic subgroup of G, and hence a normal subgroup of G.
2. Prove that the group G/G0 is abelian.
3. If N E G and G/N is abelian, prove that G0 ≤ N.
4. Prove that if H ≤ G and G0 ≤ H, then H E G
2.4 Normalisers 数学群论代考
Exercise 22 (The normaliser of a set). Let G be a group and let S ⊆ G. We define the normaliser of S in G to be NG(S) = {g ∈ G : gSg−1 = S}.
1. Prove that CG(S) ≤ NG(S) ≤ G for all S ⊆ G.
2. Let H ≤ G. Prove that H is a normal subgroup of G if and only if NG(H) = G. (We say that H is a central subgroup of G if H ⊆ Z(G). We have a similar result: H is a central subgroup of G if and only if CG(H) = G.)
3. Let H ≤ G. Prove that H E NG(H).
4. Let S ⊆ G. Prove that CG(S) E NG(S). 数学群论代考
5. Let H ≤ G. Prove that NG(H)/CG(H) is isomorphic to a subgroup of Aut(H).
Exercise 23 (The product of two subgroups). Let G be a group and let H, K ≤ G. Recall that for subsets S, T ⊆ G, we define ST = {st : s ∈ S, t ∈ T}.
1. Prove that HK is a subgroup of G if and only if HK = KH, in which case it is the unique minimal subgroup of G that contains both H and K.
2. Prove that if H ⊆ NG(K) or K ⊆ NG(H), then HK = KH and is a subgroup of G.
3. Prove that if H and K are both normal subgroups of G, then HK is a normal subgroup of G.
2.5 The universal property of quotients
Exercise 24. Let G be a group, let N be a normal subgroup of G, and let π : G → G/N be the quotient homomoprhism, which is defined by π(g) = gN for all g ∈ G. The universal property of π is the following: for every group H and every homomorphism φ : G → H such that N ≤ ker φ, there exists a unique homomorphism φ˜ : G/N → H such that φ = φ˜ ◦ π.
The universal property of π is useful for defining homomorphisms out of G/N. For each homomorphism φ : G → H with N ≤ ker φ, we obtain a map φ˜ : G/N → H that we immdiately know is a well-defined homomorphism. Sometimes we will have a formula that we would like to use to define a homomorphism ψ : G/N → H, but we do not know a priori if ψ a well-defined homomorphism. We can conclude that it is, using the universal property of π, if we can show that ψ = φ˜ for some homomorphism φ : G → H such that N ≤ ker φ. In this exercise, we will prove the universal property of π. Let H be a group and let φ : G → H be a homomorphism with N ≤ ker φ. 数学群论代考
- Suppose that there exists a homomorphism φ˜ : G/N → H such that φ = φ˜ ◦ π. Prove that for all gN ∈ G/N we have φ˜(gN) = φ(g). Conclude that φ˜ is unique if it exists.
- Prove that the map φ˜ : G/N → H defined by φ˜(gN) = φ(g) for all gN ∈ G/N is a well-definedhomomorphism such that φ = φ˜ ◦ π. Conclude that the universal property of π holds.





发表回复
要发表评论,您必须先登录。