Mathematical and Computational Sciences
MAT133Y5Y- Term Test 2
数学和计算机科学作业代写 You are not allowed to access the internet for course-related reasons, except to download and print your test, to submit you
This test contains three (3) questions. You must write your solution to each question on a separate piece of paper. Each question will be individually submitted to Crowdmark, and the transfer process must have started prior to the given deadline.
• You are allowed to use a calculator of any type.
• You are allowed to use your books and notes.
• You are expected to do the test on your own, without help from any other person.
• You are not allowed to transmit or receive information about the test from any other individual who is not a course instructor, whether in person, digitally, or by some other means.
• You are not allowed to access the internet for course-related reasons, except to download and print your test, to submit your test digitally through Crowdmark, to send an email to one of the course instructors, to access course materials, or to post a private message to the instructors through Piazza.

Unless otherwise indicated, you are required to show your work on each problem on this exam. You are expected to provide a clear explanation of your work and reasoning. The following rules apply: 数学和计算机科学作业代写
• Organize your work in a reasonably neat and coherent way, in the space provided. Work scattered all over the page without a clear ordering will receive very little credit.
• Explain your work! A correct solution will have a mixture of words and mathematics. You must convey to us that you understand the material, and this is best achieved by providing (short) explanations.
• Mysterious or unsupported answers will not receive full credit. A correct answer, unsupported by calculations, explanation, or algebraic work, will receive no credit; an incorrect answer supported by substantially correct calculations and explanations might still receive partial credit.
• If a question asks you to explain your reasoning, your answers should be short and to the point. Do not provide long, rambling explanations.
Visit https://mcs.utm.utoronto.ca/declaration/ and fill out the form there. If you do not fill out the form, you will receive a zero on this test. This should be done prior to writing the test
1. Let Sij , Tij (c) and Ui(c) be the 3 × 3 matrices that you computed in Assignment 4.
(i) (2 points) Find the determinant of Sij for all i, j.
(ii) (3 points) Find the determinant of Tij (c) for any i, j. and c ∈ R. If you are having trouble doing this in general, you can compute the determinants of T12(−1), T23(−2), and T32(2) for half of the marks. These matrices will be used in part (iv).
(iii) (3 points) Find the determinant of Ui(c) for any i and c ∈ R. If you are having trouble doing this in general, you can compute the determinants of U1(−2) and U3(1/3) for half of the marks. These matrices will be used in part (iv).
(iv) (2 points) Suppose that A is a 3 × 3 matrix and B is the matrix
B = U1(−2) T12(−1) T23(−2)U3(1/3) T32(2) S23 A
If det(B) = 6, what is det(A)?
Hint: For Question 1, you may just want to compute the determinant for all three possibilities of Sij using octave. For Questions 2 and 3, think about how we solved Question 3 from the Week 7 poll questions. In all three of these questions, your argument should not be long and complicated.
2. Geordie’s Caf´e bundles together pastry and drink items in the following way: 数学和计算机科学作业代写
• Combo 1: One cookie, one muffin, and one coffee.
• Combo 2: One muffin, one scone, and one coffee.
• Combo 3: Three cookies, three donuts, and three coffees.
• Combo 4: One cookie, one muffin, one donut, one scone, and one coffee.
• Combo 5: Two cookies, three muffins, one scone, and three coffees.
(i) (4 points) Organizers of a conference need to purchase 580 cookies, 600 muffins, 180 donuts, 200 scones, and 750 coffees for breakfast. Model this scenario as a linear system if the organizers can only purchase bundles from Geordie’s Caf´e and not individual items.
(ii) (4 points) Find all solutions to your model from part (i), then explicitly give two realistic solutions. A realistic solution is a solution consisting of nonnegative integers.
(iii) (2 points) Suppose that Geordie hires you as a consultant and asks you replace Combo 5 with a new Combo consisting of the same items (cookies, muffins, and so on), so that the organizers now have only one unique way of purchasing Combos to meet their requirements. Come up with such a Combo and show that it satisfies Geordie’s condition. Your combo does not
need to include every item, and can include as many or as few items of each item as you wish (though you may not use negative items).
3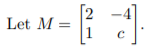
(i) (2 points) Find the inverse matrix M−1 . Note that your answer will depend on c. For what values of c is the matrix non-invertible?
(ii) (4 points) Find all values of c such that the matrix M will have λ = −2 as an eigenvalue.
(iii) (4 points) Find all values of c such that the matrix M will have v = 1 2T as an eigenvector.

更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 会计论文代写




发表回复
要发表评论,您必须先登录。