MAT401
Homework 8
函数作业代写 Show that Gal(E/Q) is a cyclic group of order 12 and determine a generator in the form τ = σa in notation analogous to the Q(ζ7)
Read: Gallian, Chapter 32 to p 536 and the Notes on Fields Extensions.
Problems: 函数作业代写
These problems are due on Crowdmark by 6pm on Wednesday, March 30th. The solutions will be discussed in tutorials that week.
- Provide the details determining the fifixed fifield of the subgroup
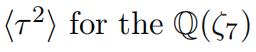 example in the notes.
example in the notes.
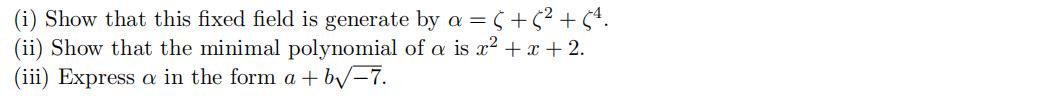
- Let E be the splitting fifield over Q of the polynomial
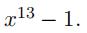 函数作业代写
函数作业代写
(i) Show that Gal(E/Q) is a cyclic group of order 12 and determine a generator in the form τ = σa in notation analogous to the Q(ζ7) example.
(ii) Write down the lattice of subgroups of Gal(E/Q).
(iii) Show that E contains a unique quadratic (i.e., degree 2) extension Q(√d) of Q and determine what it is, i.e., what is d?
- Let f(x) ∈ Q[x] be an irreducible polynomial of degree n and let E be a splitting fifield of f(x) over Q. Suppose that α is root of f(x) in E, but that Q (α) 6=
E. Show that Gal( E//Q) is not an abelian group. 函数作业代写





发表回复
要发表评论,您必须先登录。