MATH 142B Assignment 2B
代写MATH数学作业 If you use an external resource to help you complete an assignment problem, you must list this reference on your assignment.
Only complete this assignment if you have been assigned to Group B.
If you have been assigned to Group A, complete Assignment 2A instead.
• Students are welcome to discuss assignment problems with their peers and to consult external written resources in completing assignments. However, students are
not permitted to use websites or webpages dedicated to posting solutions to homework/textbook problems (including posted solutions to homework problems from other courses).
It is important that the write-up of your solutions is your own. Directly copying or paraphrasing solutions from an external resource is plagiarism. To avoid this, always write up your solutions without external aids in front of you.
• If you use an external resource to help you complete an assignment problem, you must list this reference on your assignment.
• Students must submit their assignments through Gradescope, which can be accessed through Canvas.
– Instructions for how to use Gradescope are found at gradescope.com/help
– Submissions must be correctly oriented and easily readable.
• Late assignments will not be accepted.
Only complete this assignment if you have been assigned to Group B.
If you have been assigned to Group A, complete Assignment 2A instead.
- Abbott Exercise 2.6.5.
Begin by reading the statement and proof of Theorem 2.3.4 in Lebl’s textbook.
Suppose {xn} is a convergent sequence, {yn} is a bounded sequence, and xn ≥ 0, yn ≥ 0 for every n ∈ N. Set x = lim xn and y∗ = lim sup yn.
(a) Use the theorem mentioned above to show that {xnyn} admits a subsequence converging to xy∗.
(b) Use a result from HW1A to deduce that lim sup(xnyn) = xy∗
Remark. The theorem referenced in this problem gives an alternate proof to the Bolzano-Weierstrass theorem than that given than that presented in Fitzpatrick’s textbook (which is probably the textbook you used for MATH 142A if you are in Group B).
3. Suppose {xn} is a sequence with xn 6= 0 for each n ∈ N, and set 代写MATH数学作业
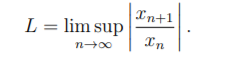
Suppose L < 1.
(a) Show that if L < a < 1, then there exists N ∈ N so that if n ≥ N, then![]()
(b) Deduce that Pxn converges.
(c) Prove that P ![]() converges.
converges.
4. (a) Abbott Exercise 2.7.8(a).
(b) Abbott Exercise 2.7.8(b).
(c) Abbott Exercise 2.7.8(c).

更多代写: HomeWork cs作业 金融代考 postgreSQL代写 IT assignment代写 统计代写 金融作业代做




发表回复
要发表评论,您必须先登录。