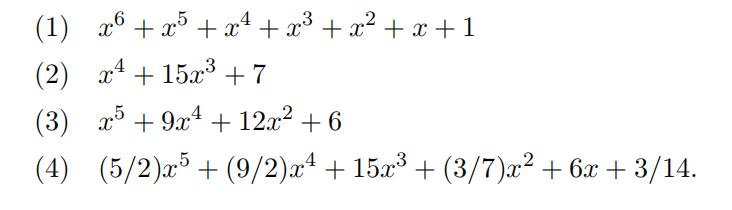
MAT401 Homework 4
代做数学Homework Determine whether or not each of the following polynomials is irreducible over Q. Explain what method you used
Read: Gallian, Chapters 17 and 18 (Omit the material on Euclidean domains)
Problems: 代做数学Homework
These problems are due on Crowdmark by 6pm on Wednesday, February 16. The solutions will be discussed in tutorials that week.
- Consider polynomials in R = Z2[x] and recall that non-constant polynomials in this ring have a unique factorization into irreducibles. In homework 3 you found the irreducibles of degree at most 3.
(i) Find all irreducible polynomials of degree 4. Explain your answer. (There are 3 of them.)
(ii) Find the factorization into irreducibles of the following polynomials:
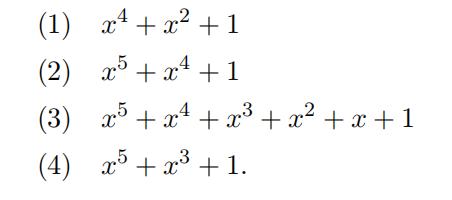
- Determine whether or not each of the following polynomials is irreducible over Q. Explain what method you used. 代做数学Homework
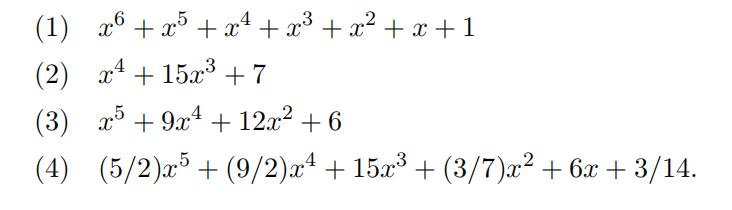
- Suppose that r is a non-zero real number such that the quantity r + 1/r is three times an integer. Show that r is irrational.
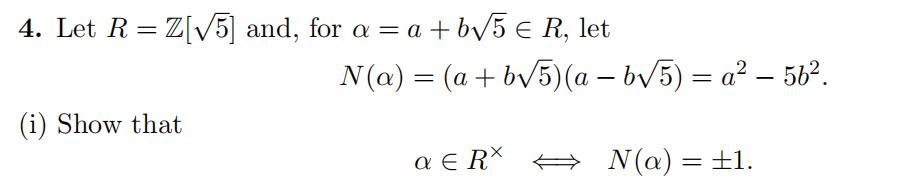
(ii) Show that the elements 2 and 1 + √ 5 are both irreducible inR.
(iii) Show that R is not a UFD. 代做数学Homework

更多代写:cs代写 经济代考 会计代写 计算机科学代写 弗拉特黑德谷社区学院代写




发表回复
要发表评论,您必须先登录。